|
Rita Ndagire Kizito
University of South Africa (UNISA)
One of the neglected elements when teaching at a distance is establishing what learners already know at the beginning of the course or module. Unlike the face-to-face environment, in distance learning there is no opportunity for administering diagnostic activities just before the onset of instruction. This means that both the weak and more advanced students receive the same level of support since there is no mechanism for differentiating their learning needs. This paper describes the characteristics of a diagnostic test aimed at determining student understanding of the basic calculus concepts of the derivative and the integral, using the mobile phone as the method of delivery. As a proof-of-concept exercise, 10 questions designed to test concept attributes and procedural knowledge involving the two basic calculus concepts were given to a sample of 30 students at the beginning of the course. The implications for curriculum design were then analysed in terms of the didactical functionalities and the communication strategy that could be developed with reference to the mobile phone.
Keywords: Prediagnostic testing; mobile phone; distance learning; undergraduate calculus teaching; Realistic Mathematics Education; didactic functionalities
Imagine the following scenario:
You are a student wanting to take a distance calculus course, but you aren’t sure that you are really up to it. It has been a while since you did your high school mathematics. You quickly access the UNISA Web site via your phone for the pretest they offer and take it. The results indicate the areas you need to revise before joining the course. You contact a social network friend who has been in a similar situation. He or she immediately texts back a message attaching an online calculus manual that you need to go through. Once home, you continue your preparations for the next pretest on your computer.
The scenario is based on the observation that mobile learning is an emerging and rapidly expanding field that provides new opportunities for learning improvement. Strictly speaking, mobile learning is a very broad term that is used in different contexts and that involves a number of mobile devices such as mobile phones, personal digital assistants (PDAs), various forms of handheld devices, and even notebooks. For the purposes of this article, I am using the term mobile learning to refer to handheld pocketsize technologies that can be put in your pocket at the point of learning. In the South African distance education environment, where the majority of students simply cannot afford access to web-based learning, the use of a mobile learning strategy seems to be a viable and rational alternative for providing instructional support.
Previously, the adoption of mobile learning was constrained by slow networks, limited services, and hesitancy on the part of organisations to invest in devices whose shelf life was too short. Mobile phone penetration and adoption were not really matched by a parallel uptake of mobile learning, despite predictions of a possible mobile learning revolution (Wagner, 2005). Reasons posited for the delay in adoption included limited and non-standardised broadband distribution capacity (Wagner, 2005), device attributes such as screen size, battery life, and security (all of which hinder learning), limited resources, and a lack of organisational acceptance (Brown, Metcalf, & Christian, 2008).
The limitation of mobile content development and distribution is slowly changing as demonstrations of the potential and actual roles of mobile technologies increase. Consumers (including distance students) who are apt mobile users have established a demand for mobile technology use. According to Traxler (2007), mobile devices are creating a new “mobile conception of society in which we are beginning to look at new ways of creating and accessing knowledge, performance, art forms, and even new economic activities” (p. 4). However, not enough research has been conducted to identify the actual functionalities that should be targeted when designing instruction using the mobile device in teaching.
Within the context of distance teaching, a neglected element is the establishment of learners’ prior knowledge at the beginning of the course or module with a view to offering the learner appropriate support. This type of diagnostic testing, prior to the onset of a learning unit or module, is slightly different from the pre-enrolment tests offered via paper (postal system), by telephone, or through prerequisite courses. While pre-enrolment testing establishes learner readiness for participating in a course, the precourse diagnostic testing is conducted to determine the amount and level of support a learner will require to advance successfully within the course. Unlike the face-to-face environment, in which a teacher has the time to briefly find out where the learners are before the course begins, in distance learning there are few opportunities for administering diagnostic activities once students have enrolled for each course or module. This means that both weak and more advanced students receive the same level of support since there is no quick mechanism for responding to individual learning needs (as would be the case in a traditional classroom). The problem is exacerbated by the large number of students enrolled in any distance learning module.
This paper describes the characteristics of a precourse diagnostic test aimed at determining initial student understanding of the basic calculus concepts of the derivative and the integral, using the mobile phone as the method of delivery. The aim of the project was to try to find out what the didactic functionalities of a simple mobile phone were and how these could be exploited to inform supporting learning mathematics at a distance. The questions posed were as follows:
There have been a number of examples of successful mobile learning interventions. For instance, Wei and Chen’s (2006) e-book interface design allowed students to enter queries on the text which were transferred to a discussion forum accessible through the mobile phone. Hartnell-Young and Vetere (2008) personalised learning by letting students capture everyday aspects of their lives in order to reconstruct their lived narratives within a classroom environment. Kinsella (2009) built a mobile application which allowed students to anonymously post questions to the teacher, who was then able to give summarised feedback to all participating students in real time. The reports from South Africa have been predominantly around the SMS “short message system” usage. These include Viljoen and Carlcook’s (2005) exploration of the experiences of adult learners’ use of SMS as a support tool while enrolled in the University of Pretoria’s distance education unit and Van Rooyen’s (2010) investigation of student responses to the integration of SMS as support tool systems in an accounting module at UNISA.
The current smart phones have multimedia conduits which, if exploited, are potentially useful for teaching and learning in many subjects. Students can collect evidence and data via audio and video recordings and by taking photographs. Students can send short text messages between mobile telephone devices or even send messages that include multimedia objects (e.g., video images and audio recordings). All these features can make a difference to the way in which students build new knowledge (Daher, 2010).
Mobile phone usage in mathematics learning is slowly increasing. For example, in their research, Yerushalmy and Ben-Zaken (2004) established that the mobile phone was a tool capable of opening up fascinating opportunities for learning because of its mobility, availability, and flexibility. Professor Yerushalmy and her team at the University of Haifa developed Java-based mathematical applications that can be installed on most mobile phones. The devices operate as minicomputers and are used for constructing graphs, solving equations, and sketching functions. Their Math4Mobile phone applications for learning algebra, geometry, and calculus can be accessed from the Web at www.math4mobile.com. This team has developed activities for elementary, middle, and high school students. Dynamic lessons where students explore mathematical concepts can be accessed from mobile phones. This means that students who have no access to classroom computers are not excluded from these learning opportunities.
On the basis of their research study, Roschelle, Patton, and Tatar (2007) claim that using mobile devices transforms the mathematics classroom into a student, assessment, knowledge, and community–centred entity. Genossar, Botzer, and Yerushalmy (2008) analysed the learning processes and experiences that occurred within a mobile phone learning environment. They found that, apart from making the dynamic mathematical applications more accessible, the mobile phone enabled students to engage in real, authentic tasks. For instance, students could record simple dynamic events with their cell phones’ video cameras and later convert the video clips into mathematical models using the mathematics applications. The mobile phone learning environment also allowed the students to work collaboratively by sharing graphs and formulae and solving problems collectively. This helped establish a community of mathematics learners. In a recent study (2010), Daher confirmed the formation of collaborative communities of budding young mathematicians. preservice teachers collected data that supported the finding that middle school student knowledge building could be fostered through learning mathematics in a mobile phone environment. Students jointly engaged in and solved authentic mathematical problems with the help of mobile phones.
In South Africa, the Meraka Institute (a research institute) has been at the forefront of the innovative use of mobile/cell phone technology to support the teaching and learning of mathematics. The Institute has been able to develop a mobile tutoring system, Doctor Maths, which runs on the MXit platform. MXit is a very popular instant-messaging service that is accessible via cell phones and that has over three million school-age subscribers. Volunteers from the Department of Engineering at the University of Pretoria offer real-time mathematical support to the high school students using the MXit chat facility on students’ cell phones at reduced rates. From an initial enrolment of just 20 students, to date the service has grown to support over 1,000 students (Van Rooyen, 2010). However, even with this evidence, it is still difficult to clearly isolate the actual functionalities that should be targeted when designing instruction using the mobile phone in teaching.
The aim of the precourse diagnostic testing carried out in this project was to determine, as quickly as possible, students’ prior knowledge of the subject at the beginning of an introductory distance calculus course. The type of pre-testing administered in this project is slightly different from the multiple-choice computerised diagnostic testing administered to determine students’ mathematical skill competencies with a view to suggesting remedial strategies (Appleby, Samuels, & Treasure-Jones, 1997). Prior research done at the undergraduate level consistently reveals that students start calculus courses with a limited view and understanding of the functional concept (Tall, 1996; Ferrini-Mundy & Lauten, 1993). In addition to this, students often exhibit cognitive difficulties when interpreting the functional concept using algebraic and graphical representations (Schnepp & Nemirvosky, 2001). The aim of this project was to ascertain if the students who enrolled for the calculus course at UNISA had an understanding of the two basic calculus concepts, the derivative and the integral, and to subsequently build on that knowledge to inform future instructional design decisions.
The use of precourse diagnostic testing in order to support student learning is not a new idea. Over the years, the recognition that students’ initial beliefs and ideas about particular phenomena form the basis of their future learning was used to design and develop diagnostic instruments to test and support student learning (Halloun & Hestenes, 1985). Currently, there are many examples of computer-assisted tutoring and testing systems (Chiou, Hwang, & Tseng, 2009; Springer & Pear, 2008). The advent of web technology has also provided us with a platform on which web-based diagnostic systems can be accessed by face-to-face and distance students alike (Bälter, 2009).
For this study, it was important to identify, as a proof-of-concept exercise, how the mobile phone could be used to enhance the learner’s experience in a way that current distance learning provision was failing to do. The main aim of the study was to establish what the didactic functionalities of a mobile phone were and how they could be exploited to inform prediagnostic testing design at a distance.
The learning transaction between teacher and student in a distance learning environment cannot occur without some form of technological mediation. The theoretical framework used in this study therefore includes ideas borrowed from two parent frameworks, an instructional design (or teaching and learning framework) together with a framework for analysing the role played by technology. The next sections are elaborations of these two frameworks; note that these two frameworks were combined for the final analysis of the project outcomes.
The prediagnostic testing in this project is part of a larger project that examines the developmental efforts required to adapt the instructional design perspective of Realistic Mathematics Education (RME) to the teaching and learning of calculus via distance education. RME was first introduced at the Freudenthal Institute in the Netherlands in the 1970s in response to a call for reform in mathematics education. RME is based on Freudenthal’s (1973; 1991) belief that mathematics education should take its point of departure in mathematics as a human activity, rather than mathematics as some sort of ready-made system. The fundamental idea is that by designing instruction in which both everyday situations and mathematical activities are mathematised, students can be helped to reinvent mathematics and (as a result) attain a better understanding of the subject.
The approach capitalises on mathematising (regarding or treating a subject or problem in mathematical terms) as a central learning activity together with guided reinvention and emergent modelling as central processes within the learning experience (Gravemeijer, 1994; Bakker, 2004; Zulkardi, 1999).
From a design perspective, the teacher needs to have some idea about where his/her students are in terms of the projected learning in order to design appropriate learning activities based on ideas that are less sophisticated than the mathematical concepts being developed. This is why the diagnostic test needed to be administered quickly. In this case, the diagnostic test was directed to getting a sense of students’ initial knowledge of the concepts of derivative and integral at the beginning of the course.
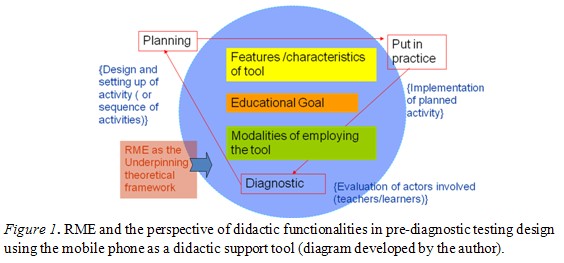
Since the transaction between teacher and student in a distance learning environment cannot occur without some form of technological mediation, a type of construct was required to analyse the role played by the technology. Cerulli, Pedemonte, and Robotti’s (2005) perspective of didactical functionalities fit well with this requirement. Cerulli et al. (2005) regard didactical functionalities as those properties (or characteristics) of a given information and communication technology (ICT) and its modalities of employment which may favour or enhance teaching and learning processes in reaction to a specific education goal.
Another construct borrowed from Cerulli et al.’s (2005) approach was the education experiment cycle (EEC) model. This was used to identify the critical phases within the project. The EEC model has three main phases: (a) the planning phase involving the setting up and sequencing of activities; (b) the putting into practice phase, in which the planned activity is implemented; and (c) the diagnostic phase, which involves evaluating the actors (teachers and students) involved. A tool’s modality of employment can be analysed in any (or only one) of the three phases, depending on the educational goal.
In order to illustrate the universality of their theory, Cerulli et al. (2005) demonstrated how the perspective of didactic functionalities could be combined with different teaching and learning theoretical frameworks in order to delineate the didactical purposes of the technological tools employed in the course of teaching and learning. Examples of the teaching and learning frameworks examined were Brousseau’s theory of didactic situations, Nardi’s version of activity theory (concentrating on computer-mediated learning), and the theory of instruments of semiotic mediation.
For this project, Cerulli et al.’s (2005) perspective of didactic functionalities and the RME approach to instructional design were combined to create a framework for designing and evaluating the precourse assessment activities. The RME framework was used to guide the design of the preassessment activities. The resulting theoretical framework, consisting of a combination of RME and the perspective of didactic functionalities, is shown in Figure 1. In terms of the perspective of didactic functionalities, the tool being considered in this research was the mobile phone within the mobile learning platform. The goal was to establish the tool’s didactic functionality. The didactic functionalities of the mobile phone were analysed in only one modality of employment, that of diagnostic testing.
A prediagnostic test aimed at determining initial student understanding of basic calculus concepts (the derivative and integral) was delivered using both print and the mobile phone. Thirty volunteer students took a 10-item prediagnostic test that was delivered using both print and the mobile phone. The students were UNISA students who had completed their first semester in a first-year calculus course. The researcher for the study was the curriculum designer, who also played an instructor role in this pilot study.
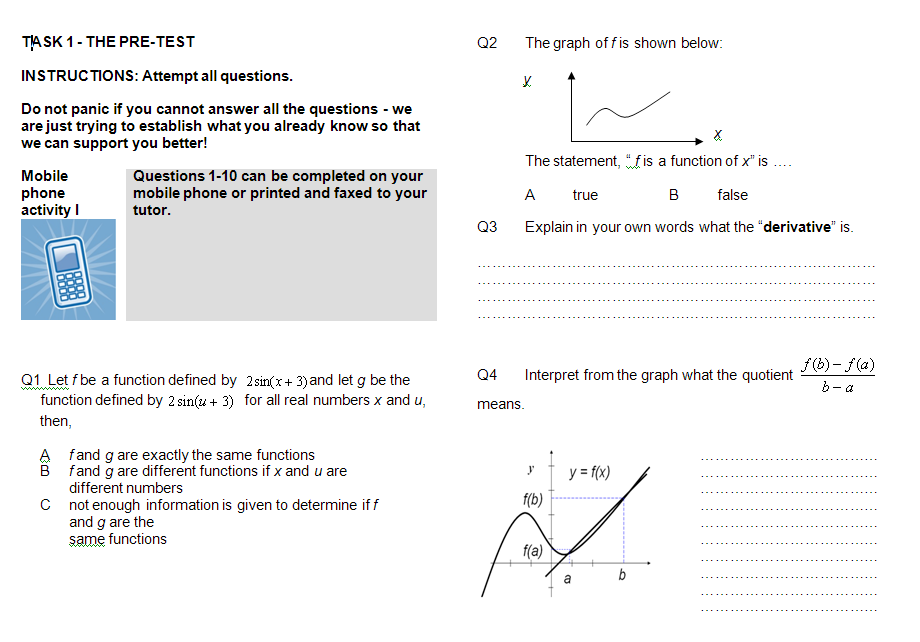
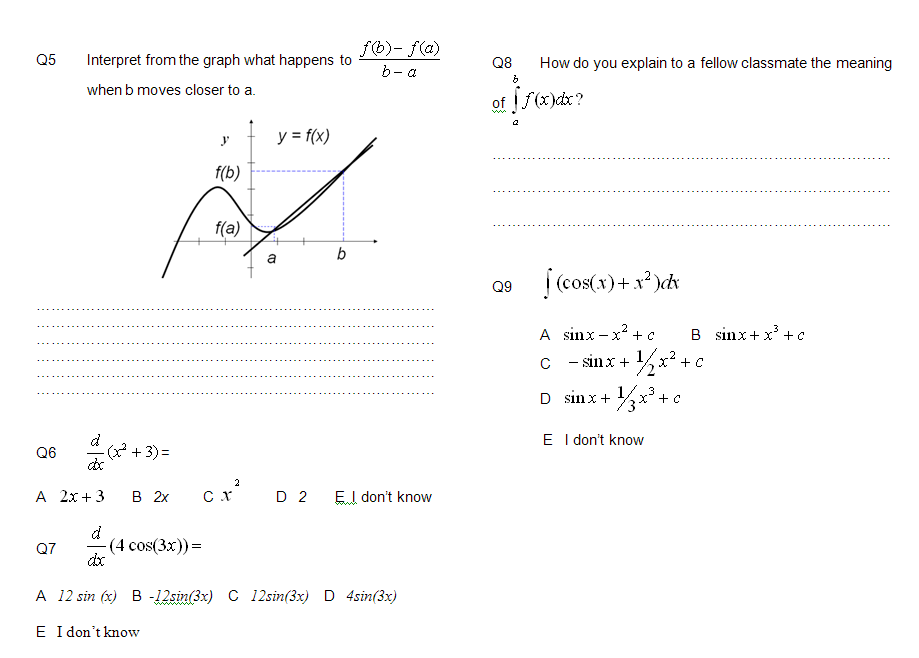
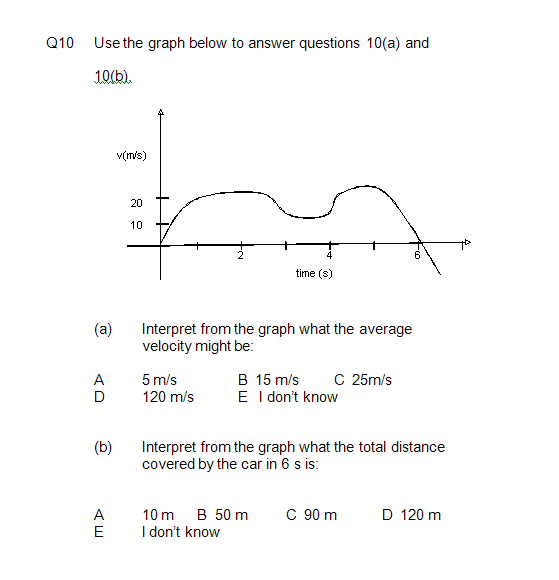
The questions were designed to gauge the students’ understanding of functions, their interpretation of graphs, and their understanding of the terms the derivative and the integral (see Appendix). Questions 1 and 2 were designed to test students’ understanding of the function and its graphical representation. Questions 3 to 7 tested students’ understanding of the derivative, including personal definitions, graphical interpretation of the concept, and use of simple formulae. Questions 8 to 9 tested students’ personal definitions of the integral and included one typical integral evaluation problem. Question 10 was designed to check the students’ understanding and graphical interpretation of both the derivative and integral concepts in relation to the average velocity and total distance covered by a moving object.
OutStart–Hot Lava Mobile, available at http://www.outstart.com/about-hot-lava-mobile.htm, was used as the learning development and management platform. Figures 2 and 3 are representations of two question items (1 and 4) as they appeared in the normal text version and the mobile phone version.

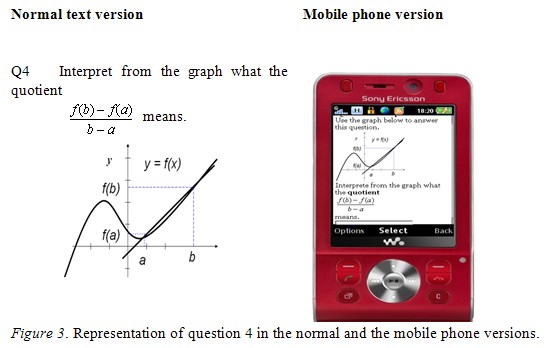
The Hot Lava software integrated an authoring system with a mobile delivery and tracking system. The integrated system of components provided a fast and efficient way of designing, creating, editing, deploying, and tracking content that could be delivered to different mobile phone models. One advantage of Hot Lava was that the content could be delivered on a variety of mobile phones. The other main advantage was its ability to track and see which students were logged in and when they registered. On individual screens, the instructor could see the order in which students attempted the questions and the number of attempts at each question before a final answer was submitted. I could also see how much time students spent on the test.
Only nine students (30%) of the group preferred to take the test on the mobile phone. Those who declined to take the test on the phone felt that they were more comfortable working with mathematics on paper. However, all of the students who took the test on the mobile indicated that they enjoyed it. There were no notable differences in terms of overall student performance on tasks. There were a few differences in terms of the number of questions completed (due to input issues), the turnaround time for receiving the answers, and the availability or nonavailability of a system for tracking student responses. Table 1 is a comparative summary of some of the findings.
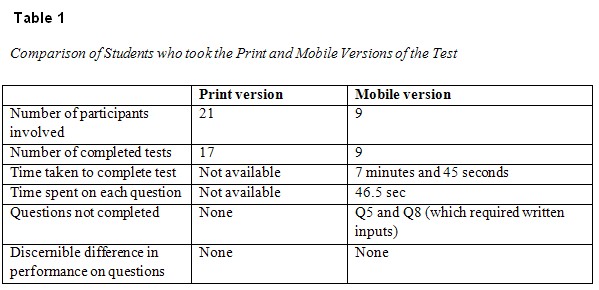
Tracking information from the Hot Lava tracking system revealed that the average time spent on the mobile test was 7 minutes and 45 seconds.
The test sought initial student interpretations of the function, the difference quotient, and the concepts of derivative and integral. The following questions were used to guide the inquiry in terms of the four constructs.
From the printed version of the test, only 17% of all participating students provided an acceptable interpretation of the concept of function.
The responses related to the difference quotient revealed that the majority of students had not yet developed a satisfactory interpretation: ![]()
For example, one student referred to the quotient as the “gradient of the tangent to curve,” even though the line drawn connecting the two points, (a, ƒ(a)) and (b, ƒ (b)), was not a tangent line. Another student defined the quotient as “the region between the graph y (ƒ (x)) and the line.” No respondent mentioned anything about the average rate of change of a function, which was what the quotient represented. A number of students said that the value of the quotient increased or the gradient became steeper as b moved close to a. The respondent who defined the quotient in terms of area said that “the area covered by the curve and the line as b moved closer to a.” One student correctly stated that “as b moves nearer to a, the gradient of the chord approaches the gradient of the curve at point (a, ƒ(a)).”
The general descriptions of the derivative given by the students depicted the derivative as an entity resulting from mathematical manipulations. Below are three examples of derivative definitions:
A derivative is a task that gets an expression out of a function and makes that found expression be a function on its own;
A derivative is a function or constant obtained from differentiating a previous function one or more times;
. . . a derivative is a mathematical equation or constant obtained after def.
All the students using the print version were able to interpret correctly the integral sign: ![]()
Responses included descriptions such as “. . . this is integration of the function (x) with respect to x between limits a and b” and “the term that means the total area between the f (x) and the x-axis within the limits b (which is the upper limit) and a (which is the lower limit) on the x-axis.” There was also a computational or procedural definition: “to integrate means to raise the power of the function f (x) by 1 and divide the top function by what you get after raising the function.” The majority of students carried out the graphical evaluations of integrals correctly.
Responses from students using the mobile version were similar to those who used the print version. Students still confused the difference quotient and the derivative. One respondent defined the difference quotient as “the gradient of the curve found from first principles, an approximate value of its gradient.” Students gave the correct interpretation of the integral and acceptable responses to Q9 and Q10, which involved graphical interpretations. The multiple question items on the mobile phone were all completed, but some of the items that required filling in were not completed. In contrast, all students completed all 10 items when using the print-based format.
Even though the sample size was quite small, one can deduce that the important didactic feature of the tool (the mobile phone) was mainly the speed and ease of tracking and analysing student responses. From this preliminary study, it was clear that the utility of the mobile phone for pre-enrolment diagnostic testing in distance learning could be enhanced if the phone was used in conjunction with a mobile phone platform such as Hot Lava. As far as the adoption of an RME perspective in the design of instruction is concerned, the phone would be useful in quickly determining a student’s starting point before embarking on any form of learning. Simple diagnostics tests could also be interjected at different teaching points during the course of learning to check student progress. In terms of student precourse testing, it seemed that the most prominent didactic functionality of the mobile phone was the speed and ease of tracking and analysing student responses.
One of the limitations of the mobile device was the students’ difficulty in handling questions that required manipulating symbols and equations. The mobile phone interfaces of the smart phones used were unable to handle this effectively. Another drawback to using the Hot Lava platform was that this platform is too expensive to maintain in a developing world context. For example, the cost for the initial testing was US$1,000 for the 30 students, and this fee did not include the additional charges required for each student registering on the Outstart–Hot Lava Web site.
Taking into account the limitations of this study (e.g., small sample size), one can draw the following conclusions:
Tim O’Reilly (2008) projects similar futuristic design ideas when he imagines future mobiles that have sensor-rich interfaces (having features such as a microphone, a camera, a touch screen, an accelerometer). These devices are also able to link to an array of cloud services that support data recognition and retrieval in order to contain assets such as voice recognition and location sensors (GPS or cell triangulation). The technology is certainly advancing very quickly, and it is therefore possible that in the near future devices and affordable systems allowing easy manipulation of symbols and more opportunities for quality student-teacher interactions will be within reach of the majority of students. For now, it becomes more efficient to make instruction design decisions based on the required human functions and make adjustments as the technology progresses.
While it is essential to understand the strengths and weaknesses of a particular technology such as the mobile phone and use this information to deploy good pedagogical practices to achieve specific learning goals, we should—as do Jay Cross, Tony O’Driscoll, and Eilif Trondsen (2007)—ask the question: “What can this technology do that will enhance the learner’s experience that my current learning provision does not?” For example, precourse assessment provision could be leveraged by organising it around a functional set of student needs, such as flexibility of symbol manipulation and affordability. One would then be able to examine the affordances the mobile device allows and map it onto students’ ease of use and course instructors’ priorities to develop relevant precourse assessment content.
In general, students preferred the paper-based tests, although they welcomed the increased opportunities for communicating with their tutor. Interviews would have to be integrated into future studies to explore in-depth perceptions of student experiences of mobile phone use. The results from this proof-of-concept project can inform the design of projects involving precourse assessment with a larger number of students. More focused research is still required to determine how best to turn the capabilities of the mobile phone into a leading component of the testing environment in distance education.
Appleby, J., Samuels, P., & Treasure-Jones, T. (1997). Diagnosys – A knowledge-based diagnostic test of basic mathematical skills. Computers and Education, 28(12), 113–131.
Bakker, A. (2004). Design research in statistics education: On symbolizing and computer tools. Utrecht: CD-ß Press.
Bakker, A., Doorman, M., & Drijvers, P. (2003). Design research on how IT may support the development of symbols and meaning in mathematics education. Retrieved from http://www.fi.uu.nl/publicaties/literatuur/5896.pdf
Bälter, O. (2009, November). Diagnostic web-based monitoring in CS1. Paper presented at the Ninth Koli Calling International Conference on Computing Education Research, Koli National Park, Finland. Retrieved from http://arachne.it.uu.se/research/publications/reports/2010-027/2010-027.pdf#page=67
Brown, J. D. M., Metcalf, D., & Christian, R. (2008, Summer). Mobile learning update. The Learning Consortium Perspective. Retrieved from http://www.masie.com/
Brousseau, G. (1997). Theory of didactical situations in mathematics (N. Balacheff, M. Cooper, R. Sutherland and V. Warfield, trans.), Kluwer, Dordrecht.
Cerulli, M., Pedemonte, B., & Robotti, E. (2005). An integrated perspective to approach technology in mathematics education. Paper presented at the CERME 4, Sant Feliu de Guíxols, Spain, 1389–1399. Retrieved from http://telearn.noe-kaleidoscope.org/warehouse/Cerulli-M-Pedemonte-P-Robotti-E-2006.pdf
Chiou, C. K., Hwang, G. J., & Tseng, J. C. R. (2009). An auto-scoring mechanism for evaluating problem-solving ability in a web-based learning environment. Computers & Education, 53(2), 261–272.
Cross, J., O’Driscoll, T., & Trondsen, E. (2007). Another life: Virtual worlds as tools for learning. Paper presented at eLearn 2007. Retrieved from http://www.reviews.com/reviewer/quickreview/frameset_toplevel.cfm?bib_id=1235515
Daher, W. (2010). Building mathematical knowledge in an authentic mobile phone environment. Australasian Journal of Educational Technology, 26(1), 85–104.
Engeström, Y. (1999). Expansive visibilization of work: An activity-theoretical perspective. Computer Supported Cooperative Work, 8(1–2), 63–93.
Ferrini-Mundy, J., & Lauten, D. (1993). Teaching and learning calculus. In P. Wilson & S. Wagner (Eds), Research ideas for the classroom: High school mathematics (pp. 117-139). New York: MacMillan.
Freudenthal, H. (1973). Mathematics as an educational task. Dordrecht: Kluwer Academic Publishers.
Freudenthal, H. (1991). Revisiting mathematics education – China lectures. Dordrecht: Kluwer Academic Publishers.
Genossar, S., Botzer, G., & Yerushalmy, M. (2008). Learning with mobile technology: A case study with students in mathematics education. International Journal of Emerging Technologies in Learning, 4(1), 23–28.
Gravemeijer, K. P. E. (1994). Educational development and educational research. Journal for Research In Mathematics Education, 25(5), 443–471.
Halloun, I., & Hestenes, D. Common sense concepts about motion. American Journal of Physics, 53, 1056–1065.
Hartnell-Young, E., & Vetere, F. (2008). A means of personalizing learning: Incorporating old and new literacies in the curriculum with mobile phones. Curriculum Journal, 19(4), 283–292.
Kinsella, S. (2009). Many to one: Using the mobile phone to interact with large classes. British Journal of Educational Technology, 40(5), 956–958.
Mariotti, M. A. (2002). Influence of technologies advances on students’ mathematical learning. In L. English, D. Tirosh, & M. Bartolini Bussi (Eds.), Handbook of international research in mathematics education (pp.73-87). LEA.
Nardi, B. A. (1996). Activity theory and human-computer interaction. In B. A. Nardi (Ed.), Context and consciousness: Activity theory and human-computer interaction (pp. 69–103). Cambridge: MIT Press.
O’Reilly, T. (2008). Voice in Google mobile app: A tipping point for the web? Retrieved from http://radar.oreilly.com/2008/11/voice-in-google-mobile-app-tipping-point.html
Roschelle, J., Patton, C., & Tatar, D. (2007). Designing networked handheld devices to enhance school learning. Advances in Computers, 70, 1–60.
Schnepp, M., & Nemirvosky, R. (2001). Constructing a foundation for the fundamental theorem of calculus. In A. Cuoco & F. Curcio (Eds.), The role of representation in school mathematics. Reston, VA: NCTM.
Springer, C. R., & Pear, J. J. (2008). Performance measures in courses using computer-aided personalized system of instruction. Computers & Education, 51(2), 829 -835.
Tall, D. (1996). Functions and calculus. In A. Bishop, K. Clements, C. Keitel, J. Kirkpatrick, & C. Laborde (Eds), The international handbook of mathematics education: Part I (pp. 289–325) . Dordrecht: Kluwer Academic Publishers.
Traxler, J. (2007). Defining, discussing and evaluating mobile learning: The moving finger writes and having writ. International Review of Research in Open and Distance Learning, 8(2). Retrieved from http://www.irrodl.org/index.php/irrodl/article/viewArticle/346
Van Rooyen, A. A. (2010). Effective integration of SMS communication into a distance education accounting module. Meditari: Research Journal of the School of Accounting Sciences, 18(1), 47–57.
Viljoen, J. D., & Carlcook, A. (2005). The case for using SMS technologies to support distance education students in South Africa: Conversations. Perspectives in Education: Research on ICTs and Education in South Africa, Special Issue, 4(23), 115–122.
Wagner, E. D. (2005). Enabling mobile learning. EDUCAUSE Review, 40(3), 40–53.
Wei , F.-S., & Chen, G.-D. (2006). Collaborative mentor support in a learning context using a ubiquitous discussion forum to facilitate knowledge sharing for lifelong learning. British Journal of Educational Technology, 37(6), 917–935.
Yerushalmy, M., & Ben-Zaken, O. (2004). Mobile phones in education: The case for Mathematics. Haifa. Retrieved from http://construct.haifa.ac.il/~michalyr/celular%20report.pdf
Zulkardi.(1999). How to design mathematics lessons based on the realistic approach. Literature Study. University of Twente. Retrieved from http://www.geocities.com/ratuilma/rme.html