
This paper reports on a case study which identifies and illustrates sources of difference in agreement in relation to reliability in a context of quantitative content analysis of a transcript of an online asynchronous discussion (OAD). Transcripts of 10 students in a month-long online asynchronous discussion were coded by two coders using an instrument with two categories, five processes, and 19 indicators of Problem Formulation and Resolution (PFR). Sources of difference were identified in relation to: coders; tasks; and students. Reliability values were calculated at the levels of categories, processes, and indicators. At the most detailed level of coding on the basis of the indicator, findings revealed that the overall level of reliability between coders was .591 when measured with Cohen’s kappa. The difference between tasks at the same level ranged from .349 to .664, and the difference between participants ranged from .390 to .907. Implications for training and research are discussed.
Keywords: content analysis; online discussions; reliability; Cohen’s kappa; sources of difference; coding
According to Berelson’s (1952) early definition, content analysis is “a research technique for the objective, systematic, and quantitative description of manifest content of communication” (p. 18). Kolbe and Burnett (1991) define it as “an observational research method that is used to systematically evaluate the symbolic content of all forms of recorded communication” (p. 243). In the context of computer conferencing, content analysis has been described as a “research methodology that uses a set of procedures to make valid inferences from text” (Kanuka and Anderson, 1998, p. 59). As with other fields of research, reliability is an essential characteristic of content analysis (Lombard, Snyder-Duch, and Bracken, 2002). In the context of content analysis of discussion transcripts, reliability is usually discussed in terms of interrater reliability, also referred to in literature as intercoder reliability, or more specifically interrater agreement, which refers to the extent of agreement between independent coders on the rating or code they assign to each object in the study (Krippendorff, 1980).
Kolbe and Burnett (1991) observed that “interjudge reliability is often perceived as the standard measure of research quality” and “[h]igh levels of disagreement among judges suggest weaknesses in research methods, including the possibility of poor operational definitions, categories, and judge training” (p. 248). Singletary (1994) suggests that reliability is “near the heart of content analysis” and argues that “if the coding is not reliable, the analysis cannot be trusted” (p. 294). Similarly, Neuendorf (2002) argues that, without establishing strong reliability, “content analysis measures are useless” (p. 141). Therefore, “if content analysts cannot demonstrate strong reliability for their findings, then people who want to apply these findings should be wary of developing implementations” (Potter and Levine-Donnerstein, 1999, p. 258).
Surprisingly, and despite agreement on the importance of reliability, it has been rarely assessed and reported in transcript analysis research in the past (Lombard et al., 2002; Neuendorf, 2002; Rourke, Anderson, Garrison, and Archer, 2001). Rourke and Anderson (2004) claim, however, that journal editors are becoming more demanding and researchers more conscientious about reporting reliability. Lombard et al. (2002) conducted a review of 200 articles on content analysis in communication research and found that, while 69 percent of them reported reliability, most provided little discussion on reliability procedures and results. Rourke et al. (2001) reviewed 19 published studies on transcript analysis of online discussions and found that, while 11 reported reliability, the majority of those studies did not provide any discussion on the issue. Additionally, of the studies that reported reliability, most used a simple percent agreement to calculate the level of agreement between coders or raters. Many methodologists, however, consider the percent agreement to be an inadequate measure of interrater reliability since it does not account for agreement between coders that is expected to happen by chance (Carletta, 1996; Lombard et al., 2002; Rourke, et al., 2001). Only three of the studies reviewed by Rourke et al. (2001) reported the use of a chance-corrected measure of interrater agreement, and in all cases, the choice was Cohen’s kappa. For a discussion on chance agreement see Potter and Levine-Donnerstein (1999).
Use of Cohen’s kappa to calculate overall reliability between two coders, however, will not provide a fine-grained measure of actual differences that might occur in coding a transcript of an Online Asynchronous Discussion (OAD) with different variables such as multiple tasks and discussants. Crocker and Schulz (2001) in a discussion of interrater reliability of manually-scored test items point attention to the need to consider sources of difference besides those between coders. These authors argued that conventional estimates of reliability do not distinguish between various sources of difference: “[a]ll are lumped together in producing an overall reliability coefficient” (Crocker and Schulz, 2001, p. 3). As an example of the types of differences they cite, task variation can be more important than scorer variation. Likewise, Neuendorf (2002) and Tinsley and Weiss (1975) argue that reliability values need to be calculated and reported for each measured variable. While this approach may not be appropriate for all contexts of quantitative content analysis, it was, for instance, adopted by Garrison, Anderson and Archer (2001) who calculated interrater reliability value for 12 indicators of social presence. The majority of studies, however, still tend to provide only the overall value of agreement between coders.
The purpose of the case study reported in this paper was to identify and illustrate sources of difference in reliability in the quantitative content analysis of a transcript of an online asynchronous discussion. Differences were investigated between two coders, eight tasks, and 10 students who we will refer to as participants in the remainder of the paper. Moreover, the extent of agreement in relation to all three variables was calculated separately for the three hierarchical levels of coding categories: two categories, five processes, and 19 indicators. Cohen’s kappa was used to calculate levels of reliability (see Cohen, 1960 for an explanation of the mechanisms of kappa). Results obtained with this measure illustrate how differences can occur, not only between coders, but as a result of other variables such as different tasks or participants. This paper discusses implications for the training of coders and for research. The background section discusses the eight tasks participants completed in the online discussion analyzed in the study. Included in this section is a description of the instrument used for the analysis of the discussion. Following the background section is a presentation of the method.
The discussion was a part of a Web-based learning module focused on engaging learners in Problem Formulation and Resolution (PFR). The un-moderated discussion was pre-structured with eight tasks or prompts including an introduction and conclusion. The six other tasks paralleled steps in a problem-solving model presented in the module. The introduction or Task 1 required participants to reflect on their initial knowledge of the problem, and compose a message in which they described their understanding of the problem. In Task 2, students were asked to describe how their understanding of the problem changed as a result of learning about how some practitioners experience the problem. Task 3 required participants to react to the reflection of at least one other participant. In Task 4, students had to compose a message to describe how their understanding of the problem had changed as a result of having read an article discussing the problem. For Task 5, participants had to react to the reflection of at least one other participant. Task 6 asked students to post a message in which they “acted on the problem”, and to suggest some ways that the problem could be dealt with “in a systematic and visible way.” In Task 7, students had to respond to a proposed action of one other participant, and to reflect on the strengths and weaknesses of the proposed action. Finally, in the conclusion or Task 8, participants were asked to describe how, in the future, as practitioners, their behavior and thinking might be different as a result of having participated in the online module.
The instrument used for coding was designed by the principal investigator (Murphy, 2004b) and represents a second iteration. This second iteration was developed after a second round of testing designed to identify instances of construct under-representation, construct irrelevance, and lack of discriminant capability in the instrument. The first iteration was developed through a conceptual framework derived from the literature and subsequent testing through the analysis of an online discussion (see Murphy, 2004a).
The coding instrument is comprised of three hierarchical levels. At the first level, there are two main categories: Problem Formulating (F) and Problem Resolution (R). The categories are further divided into processes. The category of Formulation includes two processes: Defining Problem Space (FD) and Building Knowledge (FB). The category of Resolution includes three processes: Identifying Solutions (RI); Evaluating Solutions (RE); and Acting on Solutions (RA). Finally, each of the five processes is further divided into a total of 19 specific indicators of behavior. The process of Defining Problem Space includes seven indicators, such as Agreeing with Problem as Presented in the discussion (FDA) or Identifying Causes of the Problem (FDIc), while the process of Building Knowledge includes four indicators. Under the category of Resolution, the process of Identifying Solutions (RI) includes two indicators, such as Proposing Solutions (RIP); the process of Evaluating Solutions includes four; and the final process of Acting on Solutions (RA) includes two.
Volunteer participants in the study were seven graduate and three undergraduate students. Participants identified numerically as 1, 2, and 3 were undergraduate students, whereas participants from 4 to 10 were graduate students. Participants’ involvement consisted of contributing to an online asynchronous discussion (OAD) over a one-month period. At the end of the one-month period, messages were compiled and printed copies were made of the transcripts of participants’ contribution to the discussion. During the study, participants posted a total of 84 messages, four of which were not related to the tasks and consequently excluded from the data. The syntactic unit of a paragraph within a message was chosen to be the unit of analysis for the coders (see Rourke et al., 2001, or Hillman, 1999, for a discussion on choice of unit of analysis).
Coders A and B were graduate research assistants with no prior coding experience. Their training involved one session with the principal investigator of the study, who was also a creator of the instrument. First, the principal investigator explained the instrument and demonstrated the coding procedure to the coders. Then, each coder coded the same portion of one transcript and discussed their coding decisions with the principal investigator to ensure consistent interpretation of the instrument. After the training sessions, the coders coded each transcript independently. The coders coded one transcript each day and each coding session lasted approximately one hour. The protocol adopted for coding limited coders to assigning only one possible code per unit. The total number of paragraphs in all messages posted by the students was 355. The average length of a unit of analysis, or a paragraph within a message, was 97 words. The average number of coded units for each participant was 35.5.
The coders proceeded in three stages paralleling the three hierarchical levels of the coding instrument. With each unit of analysis, coders first decided whether the participant engaged in F (defining the problem) or R (solving the problem). At the second stage, coders were required to determine in which of the processes the participant engaged. Depending on the first coding decision, they had to choose between FD and FB; if the participant engaged in F, and between RI, RE, and RA if s/he engaged in R. Finally, coders had to determine which specific type of behavior was evident in the unit, and which indicator to assign.
Instead of only reporting reliability as one aggregate measure of all coding decisions made during the content analysis, we calculated levels of reliability according to two other variables: tasks and participants. The purpose of using this fine-grained approach was to determine if some variables, such as tasks, result in a lower or higher measure than others, thus affecting the overall reliability value. In order to see how the different numbers of coding categories (two for categories, five for processes, and 19 for indicators) affected the results for the three variables (coders, tasks and participants), we calculated Cohen’s kappa coefficients on three different levels. First, we calculated levels of agreement between coders on the basis of a partial one-letter code representing either Problem Formulation (code F) or Resolution (code R) assigned by both coders to every coding unit within the transcript. Then, we calculated the agreement on the basis of a partial two-letter code representing the five processes, such as Defining Problem Space (FD) under the category of Problem Formulation, or Evaluating Solutions (RE) under the category of Problem Resolution. Finally, we calculated the level of agreement on the basis of the complete three-letter code representing the 19 indicators of behavior assigned by both coders. This third level of coding is considered to be final and complete, since it reflects all three levels of engagement in PFR presented in the instrument: whether the behavior evidenced in a particular paragraph was Problem Formulation or Resolution (F or R), which of the five processes was manifested in the unit (FD, FB, RI, RE, or RA), and in which specific PFR behavior the participant engaged, such as FBR or REC.
Cohen’s kappa (see Cohen, 1960) was chosen to calculate the levels of agreement over other reliability measures, because it accounts for agreement that is expected to occur by chance. Moreover, it is designed to measure the agreement between exactly two coders, and it can be easily calculated using accessible software. Although kappa has been criticized as being an overly conservative measure, and arbitrary in its determination of chance agreement (see for instance, Brennan and Prediger, 1981; Perreault and Leigh, 1989), it fit the purpose of this analysis. In this study, kappa coefficients were calculated using the Statistical Package for the Social Sciences (SPSS).
The purpose of this study was to identify and illustrate sources of difference in reliability in quantitative content analysis of an OAD. We could choose to report the results as one overall reliability measure for both coders across all eight tasks, 10 participants, 355 units, two categories, five processes, and 19 indicators. This coarse-grained measure would reflect the conventional approach to reporting agreement. In the case of this study, this overall value measured with Cohen’s kappa was .591. We could also choose to adopt a more fine-grained approach to reporting the reliability measures. According to this approach, we can consider results, not just as an aggregate measure, but broken down into tasks and participants. When we calculated the results in this way, the mean value of agreement reached by coders on tasks was .539, while the value of agreement coders reached on participants was .707.
Another approach to reporting the reliability measures would be to distinguish between the different levels in the instrument by reporting separate results for the categories, processes, and indicators. Using this approach, we can exclude the indicator from the calculation of agreement, focusing instead on results at the level of the process. For example, instead of considering three-letter codes assigned by coders, which represent the category (letter 1), the process (letter 2), and the indicator (letter 3), such as FDA or RIP, we only focus on the category and the process and exclude the code representing the indicator of behavior (letter 3). In this way, we consider coding decisions on a more general level – we deal with two-letter codes, such as FD and RI and calculate agreement between coders at the level of the process. At this level, the total agreement between the two coders was .724. We can also exclude both the indicator and the process from the calculations. At this level of the category, the total agreement between the coders was .825. Table 1 below provides a summary of the overall kappa coefficients of agreement between Coders A and B at the level of the category, process, and indicator (third column) as well as mean values of agreement across the eight tasks and ten participants at those three levels (fourth and fifth column). Note that the overall reliability value that would typically be reported is .591. In addition, each kappa coefficient indicating a chance-corrected level of agreement between coders is contrasted with a simple percent value of agreement. Although this study is concerned with chance-corrected reliability coefficients, we include the percent values for the readers to note the different results we would have obtained using a measure that does not correct for chance. As well, for each kappa and percent value, the table also presents the number of units on which agreement was reached by the two coders out of a total of 355 units.
Table 1. Summary of Differences in Agreement

Not only can mean results be calculated and reported at the level of the task, but they can also be considered for individual tasks at the level of the category, process, and indicator. Kappa coefficients for each of the tasks identified numerically from 1 to 8 are presented in Table 2. The total number of units that were posted throughout the discussion for each individual task is also presented. As with Table 1, for each kappa coefficient, a simple percent value of agreement, and the number of units on which coders reached an agreement are also presented. Coding at the most general level of categories produced a range in agreement between Coder A and Coder B, with the lowest value of .455 for Task 7 to the highest value of .914 for Task 6. Coding at the level of the processes produced a range from .773 for Task 1 to .407 for Task 7. Coding at the level of the indicators resulted in agreement between coders ranging from .664 for Task 2 to .349 for Task 6.
Table 2. Summary of Differences in Agreement across Tasks

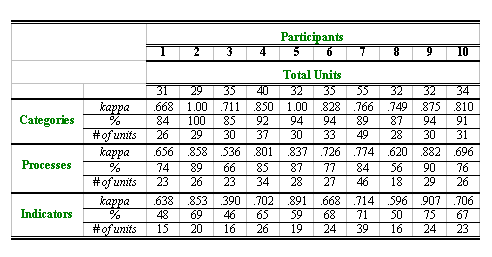
Results can be presented for individual tasks, and, as well, for individual participants. Kappa coefficients for each individual participant identified numerically are listed in Table 3. Results are presented for each of the three levels: the category, process, and indicator. The total number of units posted by each participant during the discussion is also presented. Kappa coefficients are contrasted with simple percent values, and the numbers of units in each participant’s transcript on which coders reached agreement. Coding at the level of the process resulted in a range from .882 for participant 9 to .536 for participant 3. Coding at the level of the category produced a range from .907 for participant 9 and .390 for participant 3. The highest level of agreement between Coder A and Coder B was reached for participants 2 and 5 with a value of 1.00 (perfect agreement), whereas the lowest agreement was reached for participant 1 and had a value of .668. Note that the kappa value of 1.00 was achieved even though the percentage of agreement in that case was only 94%. The reason for this discrepancy is that the kappa mechanism would not allow us to calculate agreement when, to code one variable (e.g., Task 1), one coder used a code that the other coder did not. Those unmatched codes were therefore eliminated from the analysis.
Table 3. Summary of Differences in Agreement across Participants
The previous section highlighted a fine-grained approach to the calculation of the coefficient of agreement across a range of valuables. This section of the paper aims to explain and interpret the differences in the reliability values. Prior to considering the results, we briefly discuss perspectives on rating kappa coefficients relying on terms such as high, low, and fair.
In the context of quantitative content analysis, there is no consensus as to what constitutes an acceptable level of interrater reliability (Neuendorf, 2002). As Riffe, Lacy and Fico (1998) report this lack of agreement is due to the different contexts in which the analysis can be conducted. According to Kvalseth (1989), for instance, a kappa coefficient of .61 is an indicator of high agreement, whereas Popping (1988) proposes that a value of .80 represents high overall reliability. After reviewing norms proposed by several methodologists, Neuendorf (2002) concluded that a “coefficient of .90 or greater would be acceptable to all, .80 or greater would be acceptable in most situations, and below that, there exists disagreement” (p. 145). Lombard et al. (2002), however, note that a coefficient of .70 “is often used for exploratory research” and they propose that “more liberal criteria may be used for the indices known to be more conservative” such as Cohen’s kappa (p. 593). For the purpose of this study, we adopted a scale developed by Capozzoli, McSweeney and Sinha (1999). The reason why this particular scale was chosen is that instead of providing one number that indicates acceptable reliability, it proposes kappa values that indicate three different levels of agreement: poor, fair to good, and excellent. According to Capozzoli et al.’s scale, values below .40 represent poor agreement beyond chance, values between .40 and .75 represent fair to good agreement beyond chance, and values of .75 and higher indicate excellent agreement beyond chance.
If we had reported the estimates of reliability as an overall measure using the conventional approach to reporting agreement, we would have concluded that the .591 agreement between coders using Capozzoli et al.’s (1999) scale was fair. We chose, however, to provide a more fine-grained measure of the values across a number of variables. Table 1 illustrates the mean values of agreement across coders, tasks, participants, at the level of the category, process, and indicator. The three highest values (.852, .752, and .825) were achieved at the level of the category for coders, tasks, and participants, and represented excellent agreement. The two lowest values (.591 and .539) were achieved at the level of the indicator for coders and tasks, and represented fair agreement. The third lowest value (.636) was achieved at the level of the process and represented good agreement.
The mean values of agreement between coders presented in Table 1 show that, across participants, the agreement ranged from excellent to good, and across tasks from excellent to fair. This suggests that coders reached higher agreement at the level of the participant than the task. The mean values in Tables 1, however, mask a much broader range in differences in agreement between individual tasks and individual participants. For example, as Table 3 illustrates, at the level of the indicator across ten participants, the values ranged from as low as .390 to as high as .907 or from a poor to excellent agreement. Across tasks, as presented in Table 2, however, the range went from .349 to .664 indicating a range from poor to good. If we compare mean values of agreement between tasks versus participants, we see overall fair agreement in the latter and good to excellent agreement in the former. The range of difference across participants, however, is greater than the range of difference across tasks. These results suggest that coders had more difficulty reaching agreement with tasks than with participants. Compared to the overall value of agreement for all variables, which was .591, the mean agreement of .539 across tasks was slightly lower, although both values represent only fair agreement. Compared to the overall value of .591, the mean value of .707 across participant was higher and represented good agreement.
A more detailed analysis beyond the scope of this study would be needed to explain why such a range of differences might have occurred between individual participants and between individual tasks. We can speculate that certain tasks may have elicited more easily definable behaviors than others. For example, Task 2 was designed to specifically focus participants’ attention on defining the problem. In fact, words such as ‘understanding’ were used in the instruction for that task. As with tasks, coding of some participants’ transcripts may have presented more ambiguity to the coders than others. We can note that coding Participant 3’s transcript resulted in poor agreement between coders. We might have attributed the low agreement in the coding of this transcript to the fact that this participant was one of the three undergraduate students. Coding of the other two undergraduate students’ transcripts, however, yielded good to excellent agreement.
Besides the differences in agreement across tasks and participants, we can observe a wide range of differences across all levels of the instrument – i.e., from the category to the process to the indicator. For example, Table 1 shows that the overall agreement between coders was excellent at the level of the category, agreement for the processes was good, while the agreement for the indicators was fair. Results presented in Table 2 show that agreement was higher on the categories than on the indicators. The mean results across tasks show a decline in agreement as coders move from the category to process to indicators: .752, .636, .539 respectively. Similarly, Table 3 illustrates that agreement across participants decreased as the coders moved from category to process to indicator from .825, to .738, to .707 respectively. These differences may be attributed to different factors. The first of these is the number of coding decisions.
As evidenced in Tables 2 and 3, when the number of coding decisions increased – i.e., when coders had to choose between two categories, then five processes, and then 19 indicators, the level of agreement between coders decreased. We might conclude that the increase in number of coding decision alone was enough to negatively affect agreement between coders. If we take the example of Participant 2 presented in Table 3, however, we can see that this is not the case. For all 29 units in that participant’s transcript, the coders agreed 100 percent of the time as to which of the two categories the manifested behavior should be classified. At the level of the process, the agreement remained excellent, but nonetheless declined. However, if the coders agreed on either Formulation or Resolution, at the next level of the process they did not actually have to choose between five processes, but only two if the unit had been classified as Formulation and three if the unit had been classified as Resolution. Thus, at either level – of the category or the process – there was only a possibility of either two or three decisions. If the number of coding decisions in this case did not influence the difference, we need to consider other factors that may have resulted in a difference in agreement.
One of these factors may be the discriminant capability of the categories, processes and indicators. We can assume that coders were easily able to discriminate between a behavior that represented Formulation (understanding the problem) and Resolution (solving the problem). The fact that the highest values overall were achieved at the level of the category would support this conclusion. On the other hand, they were not as effectively able to discriminate between a behavior that represented Building Knowledge and a behavior that represented Defining the Problem. This may explain why the values for the processes were lower than those for the categories. Difficulties in discriminating between indicators may account for why the reliability values were lowest at the level of the indicator. The decrease in the agreement between coders as they moved from category to process to the indicator may therefore be a result of, not only the increase in the number of coding decisions, but the inability to rely on the instrument to effectively discriminate between behaviors. While some indicators were coded for frequently (e.g. RIP - Proposing Solutions), others (e.g. RER - Rejecting Solutions Judged Unworkable) were used only once.
The higher levels of agreement at the level of the categories suggest that coders were more easily able to discriminate between behaviors related to the categories. This explanation, however, does not account for results obtained for all participants. For example, we can observe that the results for Participant 1 show only a fair agreement of .668 at the level of the categories, meaning that coders were not always able to easily decide whether a behavior manifested the discussant’s attempt to either understand or solve the problem. Using the example of one unit from this participant’s transcript, we can speculate why there may have been a difference in the choice of category for this unit. In this one unit, which was 110 words long, the participant focused both on understanding and on solving the problem. He specifically uses words such as ‘understanding’ and ‘solution.’ A reading of this 110 word unit might therefore suggest to a coder either a focus on understanding the problem and its causes, or on solving the problem. However, because the protocol adopted for coding limited coders to selecting only one code, a choice had to be made between either Formulation or Resolution. In this case, the difference in agreement appears to be due to the lack of discriminant capability of the unit of analysis. If the coders had been able to assign more than one code to a unit, or if the units had been more fine-grained, or a unit of meaning had been selected to conduct coding, coders may have been able to reach an agreement on whether the participant was engaging in Problem Formulation or Resolution. The differences in this instance may be accounted for by the lack of discriminant capability of the unit used for the analysis.
Results of the study reported on in this paper identify and illustrate a variety of sources of difference in agreement that might occur in a particular context of coding an online discussion. In the case chosen for this study, we observe that focus on many variables can provide extensive insight into the intricacies of agreement and lack of agreement that can occur in coding a discussion transcript. The study was limited by its small number of participants and the use of only one instrument. However, the differences evidenced in this one exploratory case study suggest some areas of investigation that researchers may wish to pursue.
The range in agreement across tasks shown, for example, in Table 2 indicates that, at least in this one case, coders encountered more problems with certain tasks than others. These problems may point to a need for further training focused on understanding and interpreting tasks or prompts in a discussion. As well, problems encountered in coding individual tasks may point to inherent ambiguity in the task itself. Such ambiguity could potentially be addressed by reformulating tasks. Likewise, the range of differences from poor to excellent across participants as presented in Table 3 suggests that training of coders may need to focus specifically on helping them interpret how different individuals communicate in an OAD.
In this case study, the choice of unit of analysis, as well as the discriminant capability of units and items in the instrument, also appeared to play a role in affecting agreement between coders. The choice of unit, as well as the coders’ ability to interpret units in the transcript, will likely influence levels of agreement and may need a specific focus prior to coding.
In terms of research in general, future studies might explore the issue of intrarater, in addition to interrater, reliability to gain more insight into the extent to which one coder’s interpretation affects the results obtained at two different points in time. In terms of promoting higher reliability in the coding of transcripts, it may be of value to focus specifically on the individual variables where high reliability is achieved in a particular context. For example, we can see that in the case of Participant 2 and 5, with 29 and 32 units respectively, coders reached perfect agreement. Similarly, on Task 6 coders achieved excellent agreement. A specific focus on such instances of high agreement could isolate the factors that contribute to agreement. These, in turn, could be incorporated into either training or instructions for coders. Subsequent studies might account for an explanation of the different levels of reliability for different tasks, codes, and students.
This study was made possible by a grant from the Social Sciences and Humanities Research Council of Canada (SSHRC) as well as an external Faculty of Education grant. We would like to thank Dr. Henry Schulz and Dr. Robert Crocker for their advice, and Gerry White for his assistance with calculating the reliability measures.
Berelson, B. (1952). Content analysis in communication research. New York: Free Press.
Brennan, R. L., and Prediger, D. J. (1981). Coefficient Kappa: Some uses, misuses, and alternatives. Educational and Psychological Measurement, 41, 687 – 699.
Capozzoli, M., McSweeney, L., and Sinha, D. (1999). Beyond Kappa: A review of interrater agreement measures. The Canadian Journal of Statistics, 27(1), 3 – 23.
Carletta, J. (1996). Assessing Agreement on Classification Tasks: The kappa statistic. Computational Linguistics, 22(2), 49 – 54.
Cohen, J. (1960). A coefficient of agreement for nominal scales. Educational and Psychological Measurement, 20(1), 37 – 46.
Crocker, R., and Schulz, H. (2001). Design of a generalizability study for SAIP assessments. Report submitted to the Council of Ministers of Education, Canada.
Garrison, D. R., Anderson, T., and Archer, W. (2001). Critical thinking, cognitive presence, and computer conferencing in distance education. American Journal of Distance Education, 15(1), 7 – 23.
Hillman, D. C. A. (1999). A new method for analyzing patterns of interaction. The American Journal of Distance Education, 13(2), 37 – 47.
Kanuka, H., and Anderson, T. (1998). Online social interchange, discourse, and knowledge construction. Journal of Distance Education, 13(1), 57 – 74.
Kolbe, R. H., and Burnett, M. S. (1991). Content Analysis Research: An examination of applications with directives for improving research reliability and objectivity. Journal of Consumer Research, 18, 243 – 250.
Krippendorff, K. (1980). Content Analysis: An introduction to its methodology. Beverly Hills, CA.: Sage.
Kvalseth, T. O. (1989). Note on Cohen’s kappa. Psychological Reports, 65, 223 – 226.
Lombard, M., Snyder-Duch, J., and Bracken, C. C. (2002). Content Analysis in Mass Communication: Assessment and reporting of intercoder reliability. Human Communication Research, 28, 587 – 604.
Murphy, E. (2004a). Identifying and measuring problem formulation and resolution in online asynchronous discussions. Canadian Journal of Learning and Technology, 30(1), 5 – 20.
Murphy, E. (2004b). Promoting construct validity in instruments for the analysis of transcripts of online asynchronous discussions. Educational Media International, 41(4), 346 – 354.
Neuendorf, K. A. (2002). The Content Analysis Guidebook. Thousand Oaks, CA.: Sage.
Perreault, W. D. Jr., Leigh, L. E. (1989). Reliability of nominal data based on qualitative judgments. Journal of Marketing Research, 26, 135 – 148.
Popping, R. (1988). On agreement indices for nominal data. In W. E. Saris and I. N. Gallhofer (Eds.) Sociometric Research: Volume 1, data collection and scaling (90-105). New York: St. Martin’s Press.
Potter, W. J., and Levine-Donnerstein, D. (1999). Rethinking validity and reliability in content analysis. Journal of Applied Communication Research, 27(3), 258 – 284.
Riffe, D., Lacy, S., and Fico, F. G. (1998). Analyzing Media Messages: Using quantitative content analysis in research. Mahwah, NJ.: Lawrence Erlbaum.
Rourke, L., and Anderson, T. (2004). Validity in quantitative content analysis. Educational Technology Research and Development, 52(1), 5 – 18.
Rourke, L., Anderson, T., Garrison, D. R., and Archer, W. (2001). Methodological issues in the content analysis of computer conference transcripts. International Journal of Artificial Intelligence in Education, 12(1), 8 – 22. Retrieved February 11, 2005 from: http://communitiesofinquiry.com/documents/MethPaperFinal.pdf
Singletary, M. (1994). Mass Communication Research: Contemporary methods, and applications. White Plains, NY.: Longman.
Stemler, S. E. (2004). A comparison of consensus, consistency, and measurement approaches to estimating interrater reliability. Practical Assessment, Research & Evaluation, 9(4). Retrieved April 7, 2005 from: http://PAREonline.net/getvn.asp?v=9&n=4
Tinsley, H. E., and Weiss, D. J. (1975). Interrater reliability and agreement of subjective judgments. Journal of Counseling Psychology, 22, 358 – 376.