Steven C. Shaffer
The Pennsylvania State University, USA
This paper describes systems dynamics, reviews the literature of uses of systems concepts in distance education (DE), presents a preliminary model, and ends in a call to researchers to contribute to the building of a standard model of DE.
Keywords: systems; systems theory; systems dynamics; models; theory; research
Systems theory, system dynamics, and similar phrases are often found in the literature of education, in general, and online education, in particular (Shaffer, 2004). There are two main strands of systems thought: systems theory and system dynamics. Systems theory was initially developed by biologist Ludwig von Bertalanffy (1968) as a rigorous method of describing the structure and mechanisms of organic systems. He was concerned about “the danger that general systems theory may end up in meaningless analogies” (p. 35) and was at pains to point out that “general systems theory is not a search for vague and superficial analogies” (p. 35). System dynamics (Forrester, 1968), the approach taken in this paper, comes out of the tradition of cybernetics research and is primarily focused on the dynamics of feedback loops, which, it is claimed, lie at the core of all real-world phenomena (Sterman, 2000). Sterman (1994) offers an excellent, detailed introduction to the use of systems theory in education.
Systems thought in an educational context is problematic; authors sometimes write about looking at an educational situation from “a systems perspective,” but then do not apply the tools and techniques of systems theory or system dynamics. In this paper I hope to clarify the possibilities for the use of system dynamics in the study of distance education.
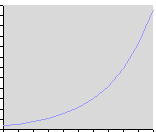
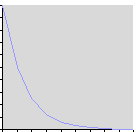
Sterman (2000) describes a dynamic system as one that inherently incorporates feedback loops. These loops are of two broad kinds, positive (self-reinforcing) and negative (damping). A common example of a positive feedback loop is any exponential growth situation – for example, a rabbit population grows exponentially in the absence of constraints (predators, food shortages, etc.), because each new generation adds to the previous generations (see Figure 1a). An example of a negative feedback loop is a boat pulling into a dock. While still a half mile away, the pilot will make large vector adjustments to steer the boat toward the destination; as the boat approaches the dock, navigational changes will become smaller and smaller (see Figure 1b). Negative feedback loops exhibit the quality of damping (decreasing the amplitude of an oscillating system), which is characteristic of goal-driven systems.
Figure 1. Two types of feedback conditions
 |
 |
Each type of system change can be described by the following causal loop diagrams. Figure 2a shows a positive reinforcement loop, indicating the total number of bunnies increases as the number of newborn bunnies increases and vice versa. Figure 2b shows the negative reinforcement loop involved in docking a boat; as the pilot approaches the dock, the difference between the current position and the goal decreases; additionally, the amount of correction that the pilot needs to make also becomes smaller.
Figure 2. Positive and negative causal loop diagrams
Figure 2a – positive reinforcement |
Figure 2b – negative reinforcement |
Real life is filled with such systems; the problem is that people do not make good inferences about even the simplest systems, even if given full information. Researchers have demonstrated this (Sterman, 2000, references specific studies) to the point that it has become a staple of organizational management seminars to demonstrate these results using simulation systems.
Adding to the complexity of any system is the human-in-the-loop, where the human is learning and thus changing the system dynamics. Most people operate in a single-loop learning mode (Figure 3a) – in this situation, the person adjusts his/ her decisions based on information feedback from the "real world," but often does not update his/ her mental models and/ or strategies. This mode can present itself as an obstinate "damn-the-torpedoes, full-speed-ahead" attitude. A more complex adaptive behavior is to adjust one's mental models and strategies as one processes feedback from experience. Thus, one might start a project with a simplistic view of the situation, but adjust one's strategy as the complexity of the situation is realized. This mode is referred to as double-loop learning (Figure 3b).
Figure 3. Examples of learning loops – adapted from Sterman, 2000
Figure 3a – Single loop learning |
Figure b – Double loop learning |
An important and confounding aspect of real-world systems is delay. There is
always some delay in receiving feedback, but the longer that delay, the harder
it is to operate effectively in it. In an educational context, feedback delay
could manifest itself in wide swings in policy; for example, administration
might fund a DE program, then cut funding too soon after launch, only later
to re-fund the program and try again. The inability of policy-makers to wait
long enough to see the results of their machinations is the cause of many strange
human system behaviors, such as real estate boom/ bust cycles, stock market
fluctuations, and aircraft pilot over-correction and oscillation.
Feedback is so pervasive that it is essentially equivalent to learning, as described for example in Vygotsky (1980, 1986). Apparently, though, most people are unable to process the entire complexity of even the simplest system. “The complexity of our mental models vastly exceeds our capacity to understand their implications” (Sterman, 2000, p. 37).
The best use of system models is in situations where controlled experiments are economically unfeasible, unethical, or impossible. The only way to work within complex contexts is to use what Sterman calls “micro-worlds”– simulations, models, etc., that allow us to “play” with the variables to see the results of various situations. Scientists and engineers do this all the time, as do airline pilots and architects. Simulations allow us to to test and comprehend the complex forces under study in ways that we would not be able to without the simulations.
There is an important difference between theory and experiment, however. We need theory to help focus our experiments and draw the results of those experiments together. This is where simulations and models can be used, but they are not an alternative to experimentation, any more than piloting a 757 flight simulator is the same as actually flying the plane. At some point, we must step out of the arena of theoretical models and move into the world of experimental evidence; it is only by doing so that we will be forced to model those messy aspects of the real world situation that might not easily fit an elegant model.
Three aspects of social systems make them inherently “loopy,” and Sterman (2000) specifically deals with these:
Policy resistance happens when agents withhold participation in an established order because it is perceived to not be in their own best interests. A well-quoted reference to this phenomenon is President Harry Truman's statement regarding incoming President Dwight Eisenhower: “He’ll sit here, and he’ll say, ‘Do this! Do that!’ And nothing will happen. Poor Ike, it won’t be a bit like the Army. He’ll find it very frustrating” (Neustadt, 1960).
The principle of bounded rationality, states that the capacity of the human mind for handling complex problems is much smaller than the size of “real world” problems, and thus the standard economic assumption of a “rational decision maker” is flawed. It replaces the standard model with the notion of satisficing: the practice of selecting and accepting a goal or solution that is good enough within the confines of limited search time and inadequate information (Hellriegel, Slocum, and Woodman, 1995, p. 622).
The law of unintended consequences is the notion that, in the absence of full knowledge of the situation (i.e., always), decisions will have effects that were not anticipated.
Creating non-simplistic system models of social systems can help to ameliorate these types of problems by giving the analyst the tools needed to grasp the outcomes of policy decisions in complex situations. The challenge is to move from generalizations to specific actionable theories with high-probability predictable outcomes. It is important to note that one can only model problems, not entire systems, because the modeler must make decisions about what aspects of the problem are salient. Full models of complex systems would be as complex as the system itself and, therefore, of no use. This is not to say that significant portions of existing models cannot be “borrowed” within other contexts, just that it is not possible to create a one-size-fits-all model of any complex social system.
According to Moore and Kearsley (1996), “It is not possible to improve quality, provide for more students, and lower costs without reorganizing education according to a systems model” (p. 7). With this in mind, the following is a review of literature on the use of systems concepts in education, starting with a brief review of a few key background references.
Considered the “father” of general systems theory, Von Bertalanffy (1968), wrote an early text that introduces the meaning and context of general systems theory (GST). Not overly technical, the book explains the genesis of the theory and describes its potential benefits to society. The author includes discussion of some of the holistic movements in various fields, such as physics (thermodynamics), psychology (Gestalt), and economics (planned economies). Our culture of specialists, he continues, is in need of generalists, but not people who simply know a little about a lot of things. Instead, what is needed are people who are well trained in a discipline that allows them to think in higher-level (more abstract) terms than is allowed for in most specialties. These people would be trained in
models, principles, and laws that apply to generalized systems or their subclasses, irrespective of their particular kind, the nature of their component elements, and the relations or 'forces' between them . . . a theory, not of systems of a more or less special kind, but of universal principles applying to systems in general (p. 32).
Strauss (2002) analyzes system theory from the standpoint of several perennial philosophic questions: (1) the one versus the many (atomism versus holism); (2) the whole-parts relationship; (3) constancy versus change; and (4) entelechy, or vital force. Of particular interest for the present paper is the question of the ontological status of a system; that is, does a system exist, or do only the parts of the system exist? For example, a university is made up of people and buildings, but does the university itself exist as an entity? If so, in what way? From a philosophic standpoint, Strauss seeks to determine if systems such as universities, calculus, and pork-belly markets have an independent existence, and what exactly the nature of that existence is. The author defends a position somewhere between the platonic and the constructivist viewpoints: he disavows the notion of pre-existing categories or forms from which particular systems (e.g., universities and labor unions) get their individual existence, and he dismisses the constructivist notion that these systems only exist in the minds of the human perceiver. His position is built upon the notion that there are different types of systems, including, at least, mathematical, spatial, kinematic, and physical. His point is that any particular system may have aspects of more than one system type, which is why complex systems defy atomization. For example, a cell will certainly have biotic system aspects, but will also have physical (chemical, molecular) and spatial aspects.
Sterman (1994) provides an excellent introduction to the concept of system dynamics within the context of learning. He declares that “the challenge facing all is how to move from generalizations about accelerated learning and systems thinking to tools and processes that help us understand complexity, design better operating policies, and guide organization- and society-wide learning” (p. 292). Certain barriers to learning are described, including dynamic complexity, limited information, confounding variables and ambiguity, misperceptions of feedback, flawed cognitive maps and causal relations, and erroneous inferences about system dynamics. The use of simulations as a necessary aspect of learning is also discussed. For example, if one tries to elicit the knowledge of an expert in order to develop a curriculum, then
regardless of the form of the model or the technique used, the results of the elicitation and mapping process is never more than a set of causal attributions, initial hypotheses about the structure of a system, which must then be tested. Simulation is the only practical way to test these models. The complexity of the cognitive maps produced by an elicitation workshop vastly exceeds our capacity to understand the implications (p. 321).
Frick (1995) applies systems theory to education and describes a plan to develop educational theory in a simulation environment. Drawing from the work of Maccia and Maccia (1966) who proposed 201 "hypotheses concerning relationships among properties of educational systems" (n.p.), Frick proposes to build software simulations of the complex interrelations within an educational system, and to use these simulations to help educators and administrators to introduce innovations into their systems.
The book chapter by Banathy and Jenlink (2004) discusses how systems approaches have been used in education; the authors refer to “the application of the intellectual technology of comprehensive systems design as an approach to the transformation of education” (p. 47) and describe how system models should be used in education research and policymaking.
One of the best known treatments of systems theory in distance education is Moore and Kearsley (1994, 2005), who offer a single-tiered taxonomy of attributes of a distance education program under the title “a systems model for distance education” (2005, p. 14). Although they clearly have a systems view in mind, diagrams of this structure can not begin to capture the full complexity of the a DE system.
Anderson (2004) offers the beginnings of a theory of online learning. The author believes that any such theory would be premature at this point, but notes that “the creation of a model is often the first step toward the development of a theory” (p. 55). This online book chapter offers such a model, which combines attributes of learning with the “affordances” of the Internet, together with a theory of the role of interaction in online learning. Building from the work of Moore, Anderson elaborates on a model of the interaction between the three “agents” in educational interactions: teacher, learner and content, creating six possible interactions (learner-teacher, teacher-content, etc.). Next, he describes a more complex model that includes the “knowledge/ content interface” (p. 49) and aspects of communication and outside support. Generally, although the author does not use the phrase system theory, this model would be a good basis on which to build a system theory of online learning. As the author summarizes, “The model presented illustrates most of the key variables that interact to create online educational experiences and contexts” (p. 55).
Saba (1999) calls for a “systems theory of distance education.” Saba and Shearer (1994) attempt to lay the groundwork for a dynamic model of distance education that can be validated empirically. The authors state that “research in distance education has been primarily program based” (p. 36) and that the few empirical studies have measured factors such as stakeholder satisfaction. They propose that in order for the field of distance education to mature, there is a need for empirical studies to verify the conceptual foundations of the field, and that system dynamics allows for modeling and predicting future states and incorporating complex political, social, and economic forces. The paper includes a discussion of the use of system dynamics modeling software to create a non-simplistic model of distance education and to begin to validate certain assumptions in the model. As the authors note, the model is still too simple, but it lays the groundwork for future work in this area. Saba (2003) sees systems theory as “the quintessential (pragmatic) tool for understanding relationships between things and not looking for a single answer to a problem within the confines of a dogma” (p. 11).
Smith and Dillon (1999) contend that systems dynamics is necessary, though not sufficient, to develop an overall model of the distance educational processes: “. . . we argue that distance education must be examined as a system, but to do so requires looking at the system and the variables that make up the system, sometimes a few at a time” (p. 34). They make an important point: one cannot have an overarching theory without some data to construct it; however, my contention is that much research is published as disembodied pieces of information that lack coherence.
Luppicini (2002) offers an overview of second-order cybernetic modeling, which “views knowing as a process of continual construction that maintains itself in the presence of (enabling or frustrating) perturbations from the medium in which it resides” (p. 93).
King and Frick (1999) present examples of using what they refer to as the SIGGS educational system modeling approach in two diverse educational settings: an elementary school classroom and a museum school. The authors discuss the complexity of the method and make an argument for its usefulness. Using their modeling approach, they demonstrate the differences between educational contexts and propose that the results of these educational situations could have been predicted from the model.
There are three common objections one encounters in conversation with educators with regard to using systems theory to inform educational practice. Each of these is briefly discussed below.
Reductionism: Sometimes systems theory is equated with a reductionist approach; this is a gross misconception. In fact, systems theory looks to model those aspects of reality which are not able to be captured in a hierarchical, reductionist framework. Modern physical science is very much taken up with non-reductionist approaches, as noted by the fact that systems theory was developed by the biologist von Bertalanffy for the very purpose of describing the complex, contextualized aspects of living systems. In my view, a tendency toward reductionism is the single largest obstacle to truly understanding the dynamics of education: variables cannot be both hierarchical and non-hierarchical within the same structure. Hierarchies are a result of reductionistic thinking. For example, even Saba, in his diagram 1.3 (Saba, 2003), while arguing for hierarchies, indicates interconnectivity among the myriad factors in multiple hierarchical levels, nullifying the very notion of those levels (which would require a single channel of input/ output interaction).
Over-simplification: Another charge against systems approaches to studying education is that, as a social system, education is too complex to study this way. Yet, every organic process can be modeled, non-simplistically, as a complex set of input/ output processes.
Behaviorism / associationism: Sometimes systems approaches are seen as a return to a behaviorist or associationist account of education. An important differentiation must be made between a strict associationism (with simple input-output pairs) and the assumption of a complex “black box,” which has inscrutable internal states (Haugeland, 2000). To the extent that we are warned against a strict associationism, this point is well taken; however, it seems possible to interpret this complaint as against modeling educational processes via their inputs and outputs, an approach that is central to all empirical research. If the alternative is to simply throw up one's hands and give up, then the only way to advance will be to recognize the possible pitfalls and move forward anyway.
I take the position that, at their base, DE variables are many and complex, and that attempts to restrain them into a hierarchy is only for our own ease of use and is eventually doomed to a false simplicity. Real-world systems are of a complexity that simple deterministic models (which were all that we could create before the advent of the computer) are doomed to fail. An obvious example of this is weather forecasting, which has made enormous strides during the last 25 years due in large part to the use of computer models (Ostby, 1999).
DE research has uncovered, perhaps, one hundred or so variables. There is a tendency by researchers, when faced with a long list of variables, to attempt to sort the list into categories – this is a natural and useful tendency when dealing with, for example, a grocery shopping list. Thus categorized, the list is a useful reference when one is in the particular areas of the grocery store (produce, frozen food, etc.).
The trouble with categorizing the list is that educational variables are interconnected, unlike most grocery items. The concept of interconnected grocery items would be typified by the following rule: Buy frozen corn only if there is no fresh corn in the produce section. This rule becomes complicating if the frozen food section comes before the produce section in one’s tour around the store – that is, during the first visit to the frozen food section, one does not know whether or not to pick up the frozen corn. The shopper has two possibilities: pick up the frozen corn and perhaps have to loop back to return it, or do not pick up the frozen corn and risk having to loop back and pick it up if no fresh corn is available in the produce section. The rule is an example of a simple coupling between variables, which would be hard to model if the list was broadly categorized as produce, frozen food, etc. In a DE context, such a rule might look like only offer courses where enrollment is 10 students or greater – there is obviously a time-delay aspect of this rule, which is impossible to capture in a static hierarchical model. Thus, our very tendency to use categorization to simplify a problem actually restricts the quality of our model. The tools of system dynamics give us the ability to handle the complexity of a problem without having to resort to power-reducing heuristics.
Modeling educational environments via system dynamics is not unheard of. Frick (1995), as discussed, puts forth a plan to develop computer software simulations of educational theory in an effort to help educators and administrators learn how to introduce innovations within their particular education systems. (See also King and Frick, 1999). If even mildly successful, such a tool would allow educational theorists and policy-makers to test out the results of their hypotheses and theories in ways that are (a) deeper than can be done via an “armchair” analysis alone, and (b) safer than testing theories on humans as a first draft. Such an approach has been used in the pharmaceutical industry for years; but it can never replace actual implementation with humans. Simulations can only help the researcher to focus on those ideas that have a higher potential for success.
Any model is an approximation; the art of modeling is incorporating all and only those things that are germane to the situation at hand. For this reason, system dynamics models can only be developed for specific situations – they do not allow for the creation of a “unified theory of everything.” Full models of complex systems would necessarily end up being as complex as the system itself.
DE can be well modeled via system dynamics, specifically because of the capacity of system dynamics to capture the small-changes-cause-large-effects nature of systems. If one breaks an educational system into, say, five easy pieces, that system will not be able to exhibit complex behavior, and thus any modeling of DE, for example, will stay encapsulated within its hierarchical category and not affect the system as a whole. By separately modeling dozens or hundreds of interacting variables within a system, however, it is possible to witness emergent behavior of the whole system. The notion of emergent behavior is central to current systems thinking (Crutchfield and Mitchell, 1994), but can only happen within the context of a system of sufficient complexity. The collapse of the Tacoma Narrows Bridge in 1940 illustrates how a small factor can grow into a major changing force in an existing environment (see http://abel.math.harvard.edu/ archive/21b_fall_03/tacoma/ for a video clip). A relatively small force of wind (35 – 46 mph) at the resonance frequency of the bridge caused the bridge to sway wildly and eventually collapse. At the time the bridge was built, engineers did not have a clear understanding of the complexity of forces at work on a suspension bridge; after the collapse, they learned more. With regard to education, it is my hope that we do not have to wait for a collapse before we learn more; for example, DE administration could model the effects of re-routing funding from one area to another and attempt to determine the effects before implementing the policy.
Many of us have become acutely aware that there is no accepted theory of anything in DE. There are many theories, but each new paper seems to come with permission to question or ignore everything that has come before (Moore, 2004). With the plethora of research that is available, it seems to me that we are ready to start sifting the wheat from the chaff.
I propose that the distance education community work together to create a model of what is known and/ or generally accepted in the field, and to hone the model by subjecting it to scrutiny and enhancement by volunteers. In many ways this project will emulate the open source movement in software development, where for example, Linus Torvalds created the kernel of Linux, and the rest of the program has been built by groups of volunteers improving on each other’s work to make a cohesive whole (Weber, 2004). I propose a similar process for developing a DE model, and have created a web site called communityofscholars.net in which to collaborate on this project. In order to “kick start” this process, I propose the following preliminary model – absolutely no pretense of completeness or correctness is implied.
Based to a large extent on Arai (1995) , I present a preliminary model of the socio-economic macro environment of distance education in Figure 4. (A full explanation of the justification of the model is available on the website.) The value of this model is twofold: (1) it tries to lay out the complexity of the economic relationships which form the environment of a distance education program and (2) it helps to focus research on distance education program design (more on this below). Several notational aspects of this diagram need to be explained: (a) non-shaded rectangles indicate aspects of the system which are not directly measurable; (b) non-shaded ovals indicate aspects of the system which are directly measurable; and (c) the two shaded areas indicate central foci for the following discussion. Also it is important to note that this model is not presented using causal loop diagrams because not enough information is yet available to make this practical. Each arrow in this model is an opportunity for research – we need to know what these relationships are and even if they exist or not.
Figure 4. Preliminary model of the socio-economic environment of DE
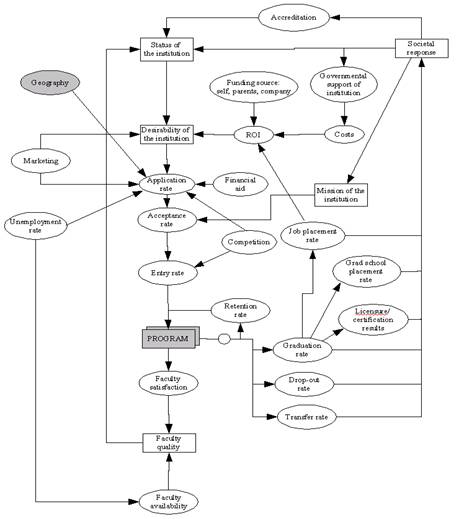
One aspect of this model is that there is very little which makes it specific to distance education; in fact, the only difference is the notion of geography, which can be manipulated by adjusting the attribute parameters – making distance higher education equivalent to face-to-face instruction for the purposes of determining the macro-environmental influences. This has broad implications for DE research since, if this relationship holds, this means that all research in higher education at this level of abstraction will also apply to DE research.
Another important aspect of this preliminary model is that the notion of program has been abstracted out of the model. This means that particular aspects of a DE program can be seen to act as a “plug in module” for the model, which means that the internal aspects of a program do not directly affect the environment except through the five output variables shown (retention rate, graduation rate, drop-out rate, transfer rate and faculty satisfaction). These output variables – all of which are measurable – have a complex, dynamic relationship with the rest of the system and thus these relationships are not easy to define. Some relationship between these program outputs and the single input to the program – entrance rate – can serve as a definition of the answer to the question is program x better than program y? One should not assume that the measure of a good program is that it accepts many students, however, because this might lead to time-delayed consequences of moving the program into disfavor. This kind of dynamic can be seen when certain academic departments are well regarded and then slowly lose that regard based on administrative decisions made.
If the assumptions of this model hold, the ramifications for DE research are important: it will allow researchers who are interested primarily in program design and pedagogy to focus on the six variables (entry rate plus the five output variables) as the environmental inputs and outputs of the system. This will give DE program researchers a consistent means of comparing results.
However, this model is not sufficient; it is presented simply to give an illustration of what such a model might look like. Each relation – indeed attributes and relations that are not even shown – needs to be fully studied and a research-based consensus built regarding the status of each. As these relationships are identified and verified, the DE research community can stop re-creating theory with each new publication.
My goal is for the communityofscholars.net site to act as a conduit for the development of a system dynamics model of distance education, and each contributor will get equal billing on the project. I have laid out some initial ideas here and on the site, but these may be overridden by analysis and empirical data. This project is not entirely selfless; I strongly desire a more stable base of theory within which to perform my research. Can DE researchers work together to develop a non-trivial, standard model of the field? My hope is that we can; my intention is to report on our progress in periodic updates.
Anderson, T. (2004). Toward a theory of online learning, in T. Anderson and
F.Elloumi (Eds.) Theory and Practice of Online Learning (p. 33-60).
Retrieved April 15, 2004 from: http://cde.athabascau.ca/online_book/
Arai, K. (1995). The Economics of Education: An anlysis of college-going
behavior. Tokyo: Springer.
Banathy, B. H., and Jenlink, P. M. (2004). Systems inquiry and its application
in education. In D. H. Jonassen (Ed.) Handbook of Research on Educational
Communications and Technology (p. 37- 57). Mahwah, NJ.: Lawrence Erlbaum.
Crutchfield, J., and Mitchell, M. (1994). The Evolution of Emergent Computation.
Santa Fe Institute Technical Reports. Santa Fe, NM.: Santa Fe Institute.
Forrester, J. W. (1968). Principles of Systems. Cambridge, MA.: Productivity
Press.
Frick, T. (1995). Understanding Systemic Change in Education. Retrieved
August 2004, from: http://education.indiana.edu/ist/courses/r
695fric.html
Haugeland, J. (2000). What is Mind Design? In Mind Design II: Philosophy,
Psychology, Artificial Intelligence. Cambridge, MA.: MIT Press.
Hellriegel, D., Slocum, J., and Woodman, R. (1995). Organizational Behavior.
Minneapolis MN.: West.
King, K., and Frick, T. (1999). Transforming Education: Case studies in systems
thinking. Paper presented at the annual meeting of the American Educational
Research Association, April 21-23. Montreal, Canada.
Luppicini, R. J. (2002). Toward a conversation system modeling research methodology
for studying computer-mediated learning communities. Journal of Distance
Education, 17(2), 87 – 101.
Maccia, E., and Maccia G. (1966). Development of Educational Theory Derived
from Three Theory Models. Washington, DC.: U.S. Office of Education, project
No. 5-0638. Retrieved October 7, 2005 from: http://education.indiana.edu/~frick/edutheo.html
Moore, M., and Kearsley, G. (1996/2005). Distance Education: A systems view.
Belmont, CA.: Wadsworth.
Moore, M. (2004). Research Worth Rublishing. American Journal of Distance
Education, 18(3), 127 – 130.
Neustadt, R. (1960). Presidential Power: the politics of leadership. Retrieved
April 15, 2005 from: http://www.bartleby.com/73/1514.html
Ostby, F. (1999). Improved Accuracy in Severe Storm Forecasting by the Severe
Local Storms Unit During the Last 25 years: Then versus now. Weather and
Forecasting, 14(8), 526 – 543.
Saba, F., and Shearer, R. (1994). Verifying key theoretical concepts in a dynamic
model of distance education. American Journal of Distance Education, 8(1),
36 – 59.
Saba, F. (2003). Distance Education Theory, Methodology and Epistemology: A
pragmatic paradigm. In M. Moore and W. Anderson (Eds.) Handbook of Distance
Education, (p 3-20). Mahwah, NJ.: Lawrence Erlbaum.
Saba, F. (1999). Toward a Systems Theory of Distance Education. American
Journal of Distance Education, 13(2), 24 – 31.
Shaffer, S. (2004). The Uses of Systems Theory in Distance Education: An annotated
bibliography. DEOS News 13(7). Retrieved October 7, 2005 from: http://www.ed.psu.edu/acsde/deos/deosnews/deosnews13_7.pdf
Smith, P., and Dillon, C. (1999). Toward a Systems Theory of Distance Education:
A response. American Journal of Distance Education, 13(2), 32 –
36.
Sterman, J. (1994). Learning in and about complex systems. System Dynamics
Review, 10(2-3), 291 – 330.
Sterman, J. (2000). Business Dynamics: Systems thinking and modeling for
a complex world. Boston, MA.: McGraw-Hill Irwin.
Strauss, D. (2002). The scope and limitations of von Bertalanffy's systems theory.
South African Journal of Philosophy, 21(3), 163 – 179.
von Bertalanffy, L. (1968). General Systems Theory: Foundations, development,
applications. New York: George Braziller.
Vygotsky, L. (1980). Mind in Society: The development of the higher psychological
processes. Cambridge, MA.: Harvard University Press.
Vygotsky, L. (1986). Thought and Language. Cambridge, MA.: MIT Press.
Weber, S. (2004). The Success of Open Source. Cambridge, MA.: Harvard
University Press.