Volume 22, Number 3
Gaël Nongni, PhD
Faculty of Educational Sciences, Université Laval, Canada
The scientific literature identifies five challenges related to training teachers: the basics of the constructivist approach, the problematization of mathematical knowledge to be taught, the promotion of interdisciplinarity, the use of digital pedagogical resources in planning teaching, and new skills to be developed due to the arrival of artificial intelligence. Considering the COVID-19 pandemic, it is appropriate to consider a sixth challenge, notably, training teachers capable of delivering mathematical distance learning courses focused on students’ conceptual understanding. It therefore is necessary to link the stakes of initial training with that of distance learning, which can enhance conceptual understanding. Linking the need to construct knowledge among students with technological tools used for distance learning allows new challenges faced in the planning of mathematics teaching to be highlighted. These new challenges give rise to the anticipation genesis that helps in situating the planning of mathematics teaching between three variables: artifact variables, arrangement variables, and variables related to the nature of the data to be used. These variables are a major asset for the training of the preservice mathematics teacher. Their study in this article allows us to recognize that the choice of technological tools to be used in mathematics distance learning depends greatly on the conceptual analysis of the mathematical knowledge to be taught. This study shows that it is important to rethink and question distance learning for each mathematical concept.
Keywords: distance learning, planning, preservice teachers, conceptual understanding, mathematics
The COVID-19 pandemic has had a significant impact on education in most countries around the world. Governments have temporarily closed all schools. According to UNESCO, the closure affects more than 91.5% of the world’s student population and 63 million teachers, a figure that might increase before the end of the crisis. On March 20, 2020, UNESCO organized a first webinar with government officials and education experts from 50 countries to encourage school continuity and learning in particular. This illustrates the importance of “adopting a community-wide approach and strengthening partnerships to ensure inclusive distance learning” (UNESCO, 2020a). Distance learning is a teaching/learning system in which the teacher and students are separated geographically (Rogers, 2009). On March 27, 2020, a second webinar gathering 159 participants from 33 countries from all regions of the world was organized by UNESCO. The latter focused on teacher training and support and highlighted that the suddenness of school closures took most teachers around the world by surprise (UNESCO, 2020b).
The states of the world have used various strategies depending on their different resources. In Quebec, the response was diversified. First came government measures, such as creating a national learning platform (L’école Ouverte: https://www.ecoleouverte.ca/fr/?) for students, parents, and teachers; proposing weekly educational kits in schools; and partnering with local television stations to promote TV learning and partnerships with educational content providers, some of which have focused on distance learning. In addition, we have observed the purchase of computer and technological tools necessary to allow all students in Quebec to easily continue learning at home. Then we have measures taken by school centres such as synchronous or asynchronous distance learning. Schools have not only respected the measures proposed by the government, but they have also used and continue to use creativity in order to continue distance learning and to make the necessary changes to diversify human and material resources. For example, several virtual schools have been created and are recruiting new pedagogical advisers to support in-service teachers. Finally, we have nonprofit organizations and private companies tutoring or designing educational content that offer contents to students and synchronous distance learning environments.
Parents, students, and teachers are thus called upon to adapt to distance learning. They should therefore consider a new way of learning, teaching, and collaborating during the confinement period. This raises several questions. Have teachers been trained to deal with such situations that require them to teach remotely? We observed that the Ministry of Education and Higher Education of Quebec, in partnership with TéLUQ University, has equipped teachers from elementary school to university with global practices of distance learning through an asynchronous firmware: J’enseigne à distance (https://www.teluq.ca/site/etudes/clom/enseigne-a-distance.php). In addition, RECIT’s national services enrich the provision of in-service teacher training by offering webinars in the form of distance learning focusing on disciplines.i However, although there is a strong demand for teachers who require coaching and support on distance learning, RECIT’s national services can only accommodate a limited number of teachers in their training. Thus, the government of Quebec has increased the number of RECIT educational advisers so that they can accompany many in-service teachers on the pedagogical strategies and the use of the tools for distance learning. However, analyzing the different educational resources available to support teachers allows us to notice that very few of them deal with distance teaching in a disciplinary way. In addition, the strong demand for in-service training on pedagogy and didactics of distance learning raises questions about mathematics teachers’ initial training: how does teachers’ initial training prepare preservice teachers for planning mathematics distance learning?
To answer this question, it is essential to analyze previous studies on teaching and learning mathematical concepts at a distance. However, several of these studies have been interested in the use of tools, environments, and online platforms for teaching and assessing mathematics (Cho & Heron, 2015; Farrús & Costa-jussà, 2013; Ku et al., 2011; Lee, 2014), but few studies have been interested in distance teaching of mathematics, focused on the construction of knowledge in students (Francis & Jacobsen, 2013). In this work, we will define, in an innovative way, the parameters that operationalize the planning of mathematics distance learning anchored in the construction of knowledge in students. Our research objective is therefore to define a theoretical framework to fuel teachers’ initial training in the planning of mathematics distance learning.
Our research question concerns the training of teachers so that they are able to provide distance learning by relying on, among other things, creativity, collaboration, and the development of conceptual understanding among students. As part of this work, we will answer the following question: How does initial training prepare preservice teachers for planning distance learning focused on developing students’ conceptual understanding? Our analysis will be carried out mainly through examining scientific research on mathematics distance learning over the past 20 years. This will also help to define more precisely the new challenges related to the initial training of mathematics teachers.
The mathematics distance teaching and learning process should not be viewed in the same way as that of other disciplines. The type of support required for the mathematics teaching and learning process goes far beyond staying in contact with mathematics. It must above all consider the development of students’ conceptual understanding. Indeed, it is important not to confuse transposed distance learning in emergency situations with teaching that is truly planned to be delivered from a distance (Hodges et al., 2020). During the COVID-19 pandemic, we observed in most countries that applied confinement measures how schools concerned with student learning improvised several strategies enabling students to continue practising mathematics—for example, sending homework assignments through e-mail, as well as asynchronous and synchronous courses. Although these learning continuity strategies that were improvised according to diverse educational resources available are highly appreciated, it appears that secondary education teachers were not prepared to face such a crisis. This means to encourage their students’ knowledge building through distance learning. This shows the need to anticipate these problems at the level of initial training. During initial training, these anticipations require multiple “moments and places of ‘discussion’ about different knowledges enriching the teaching practice” (Malo, 2000, p. 233). Thus, three phases are considered from these discussions surrounding the initial training of mathematics teachers: the distance learning planning phase, the distance learning phase, and the distance assessment phase. In this work, we will focus on the planning phase of mathematics distance learning.
In their planning, secondary preservice teachers may find it difficult to establish coherence between the skills to build in students and the questions to ask in anticipation activities (Diallo, 2005). In particular, they have difficulty transferring the didactic knowledge they have learned to adapt their planning to the students’ level and to transform mathematical knowledge into an object of teaching by establishing links between concepts (Morin, 2008). They also have difficulty reflecting on teaching objectives such as formulating learning objectives, developing assessment approaches, and adapting their teaching to students’ needs (Clerc & Martin, 2011; Cohan & Honigsfeld, 2006; Nongni, 2020). In terms of resource evaluation, some preservice teachers appear to have difficulty assessing the relevance of the digital resources they use to enrich their teaching planning (Dumouchel & Karsenti, 2013).
Several factors in teachers’ initial training influence these difficulties, including links between practical and theoretical training, the place given to analyzing mathematical concepts, and the analysis of digital technology specificities in the development of conceptual understanding, notably for face-to-face training and distance learning. These difficulties point to the need to study the planning of mathematics distance learning. Indeed, when planning mathematics distance learning, the constraints of conceptual understanding must be considered by promoting the development of mathematical thinking and reasoning among students. It is important for preservice teachers to be aware that distance learning is intended to contribute to the construction of knowledge in students. The teachers must therefore see the relevance of developing an overview of the goals and issues involved in planning mathematics distance learning.
The anticipation phase in the distance learning of a mathematical concept takes place before students encounter the teaching subject. It must account for previous learning sequences and constraints of available resources that can support the teaching and that can be involved in students’ learning process. This anticipation phase helps in providing adaptations that will enable effective control of the work environment (Cabon et al., 2014). The anticipation phase is characterized by thinking and decision-making approaches regarding the teaching to be provided and the learning, whereby the teacher has a great responsibility as far as improvisation and adaptation are concerned (Tochon, 2013). Moreover, Bergeron (2016) and Legendre (2005) define planning as an anticipation process made up of course preparation operations that take into account teachers’ creativity, unpredictable elements, students’ learning needs, resources required for teaching, and the analysis of teaching situations. Thus, subject to a variety of educational resources, activities experienced by preservice teachers relate directly to anticipation activities, and the educational resource they design becomes their planning (Nongni, 2020). It is therefore appropriate to define the requirements related to anticipation activities during initial training, especially when preservice teachers use various educational resources to develop planning.
In this perspective, Rabardel (1995) studies the artifact-instrument dialectic by supporting the thesis that analyzing an artifact’s conceptual properties is necessary to achieve teaching goals. An artifact is a resource capable of interfering with or “nurturing” teaching practice (Adler, 2010). Indeed, the analysis of the conceptual properties of an artifact leads to the elaboration of use patterns, a concept borrowed from Vergnaud (1994). Vergnaud (1994) calls a use pattern a structured organization of a subject’s action. Use patterns allow one to carry out a task and to anticipate and plan one’s activity (Vergnaud, 1990). Thus, the artifact and use patterns constitute a mixed entity, allowing for the emergence of what Rabardel (1999) calls an instrument: instrumental genesis. Considering the diversity of the resources, Gueudet and Trouche (2008) extend Rabardel’s (1995) instrumental approach by recognizing the importance of documentary work in planning mathematics teaching. Gueudet and Trouche (2008) extend the artifact-instrument dialectic from the instrumental approach to the resource-document dialectic. For them, a document is made up of two components: recombined resources plus use patterns. We consider resources, including digital and non-digital (software, applications, books, course materials, interactions, etc.), in a broad sense (Adler, 2000). The process of transforming a resource into a document is the documentary genesis (Gueudet & Trouche, 2008). This new dialectic makes it possible to manipulate didactic knowledge and knowledge related to the activity and professional development of preservice teachers. However, the documentary genesis does not consider the epistemological stance adopted by future teachers when they operationalize their anticipation activity. Indeed, a change in stance is necessary to offer distance learning that contributes to developing learners’ skills (CSE, 2020). It becomes important to define a genesis that considers changing stances during anticipation activities when planning mathematics distance learning.
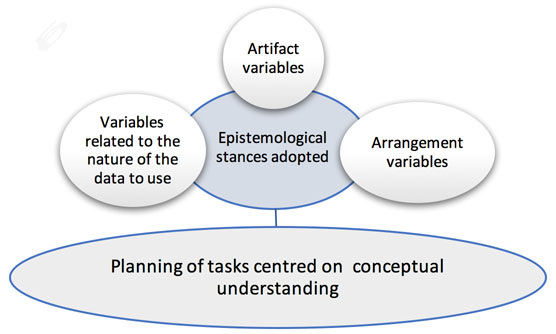
Anticipation activities range between the search for digital educational resources and the design of planning (Nongni, 2020). They are operationalized through artifact variables, arrangement variables, and variables related to the nature of the data to be used (Nongni, 2020). These are variables brought about when preparing for mathematics distance learning. Artifact variables make up a scenario system associated with the research, collection, evaluation, design, revision, and analysis of resources involved in teaching practice (Gueudet & Trouche, 2010). Arrangement variables make up a system of educational operating scenarios connected with the knowledge to build using artifacts (Trouche, 2007). They consist of patterns of use and their functioning, their evolution by accommodation or assimilation, and their joint evolution with the mathematical knowledge to teach. Variables related to the nature of the data to be used reflect all parameters that affect the data to promote students’ knowledge building when teaching, such as didactic variables, data from reality, and data collected by students. Didactic variables are parameters that can be modified by the teacher. Their modifications (even limited) are likely to influence students’ problem-solving process (Brousseau, 1998).
In addition to the previously defined variables, it is important to consider epistemological stances adopted by preservice teachers during anticipation activities (DeBlois, 2012; DeBlois & Squalli, 2002) when planning distance learning. In fact, Nongni (2020) has noted that the epistemological stance adopted by preservice teachers has an impact on their anticipation activities. Nongni (2020) also noticed that anticipation activities lead trainees to reconsider their knowledge, teaching, and learning problems in a dynamic perspective. So mathematical and technological skills, teaching conceptions, and their development vary from one stance to another, particularly between the stances of the former student, the university student, and the teacher. Conceptions about teaching correspond to “personal approaches to mathematics teaching. This includes mental images representing typical learning and teaching activities as well as the underlying principles” (Gattuso, 1993, p. 220). The former student’s stance helps in maintaining conceptions about mathematics and its learning (DeBlois & Squalli, 2002). Conceptions about mathematics “bring together all personal beliefs about what mathematics is and what it means to do mathematics” (Gattuso, 1993, p. 219). The former student’s stance includes teaching problems for which answers are available, learning of mathematics through memorization, and fear or resistance when it comes to dealing with teaching approaches (DeBlois, 2012; DeBlois & Squalli, 2002; Nongni, 2020). This stance also includes personal beliefs about mathematics distance learning. The university student’s stance highlights difficulties that can transform the teaching project by distancing the former student from their experiences (DeBlois & Squalli, 2002). It is characterized by the knowledge acquired while training, such as practices discussed during university didactic courses and didactic knowledge offered to preservice teachers (Savard, 2014). This didactic knowledge considers the analysis of tasks and educational material that can promote conceptual understanding when teaching mathematics remotely. The teacher’s stance is observed when the concerns of preservice teachers are focused on student learning (Deblois, 2012; DeBlois & Squalli, 2002; Ndolly, 2012). The stances previously explained justify and define the support needed by preservice teachers in anticipation activities in mathematics distance teaching. As a matter of fact, The preservice teachers need to think more deeply about how distance learning resources should be used to encourage student motivation, to represent, design, and explore mathematical ideas to help students build mathematical concepts.
Mathematics teachers’ initial training should include anticipations that could allow transitions from one epistemological stance to another, especially to encourage the emergence of the teacher’s stance. This transition requires considering variables that may contribute to students’ knowledge construction during distance learning, notably artifact variables, arrangement variables, and variables related to the nature of the data. This genesis, which values, among others, the emergence of the teacher’s stance among preservice teachers through these three variables is called anticipation genesis.
Artifact variables of anticipation genesis for distance learning are operationalized by the choice and analysis of resources to be used, the combination of resources, the canvas for the combination of several resources, the appropriation of teaching-learning environments, the analysis of content to be taught according to selected teaching-learning environments, the design of teaching materials, the design of both formative and summative assessments, and the continuous evaluation and revision of teaching-learning environments (Nongni, 2020). We have observed that not only are artifact variables limited to the choice or recension of technological tools for synchronous or asynchronous mathematics teaching, but these effects also take account of the analysis and revision of technological tools based on the teaching content and the students’ familiarity with the learning environment. This operationalization of artifact variables for distance learning promotes the emergence of the teacher’s stance among mathematics preservice teachers, mainly by considering teaching-learning problems in a more dynamic perspective.
In fact, choosing distance learning tools first requires a conceptual analysis of the concepts to teach. The nature of the mathematical task to be taught therefore influences the technology to be used (Francis & Jacobsen, 2013). In an online synchronous learning community involving 13 Canadian mathematics teaching professionals exploring how to teach better, Francis and Jacobsen (2013) observe that mathematical tasks that require a minimum of symbolic writing appear to work better in online learning environments. It is therefore important, in distance learning planning, to anticipate the challenges linked to technological tools by diagnosing opportunities provided such as possible interactions with learners and with mathematics (Francis & Jacobsen, 2013). A distance learning environment should have flexibility in terms of face-to-face teaching, especially in communicating, manipulating, using, and visualizing mathematical symbols or representations. However, it is through analyzing the concept being taught that we determine, inter alia, technological tools that could be used for distance learning and the way in which pedagogical design employing these technological tools is carried out. This is how we move towards distance learning focused on conceptual understanding. On the contrary, if the technological tool is chosen before the conceptual analysis, teaching could be limited to putting students in contact with mathematics. We then differentiate between learning mathematics remotely and putting in contact with mathematics.
The appropriation of teaching and learning environments by preservice teachers is an effect of artifact variables, which could contribute to the emergence of the teacher’s stance among them. In effect, students appear more motivated when the teacher has better mastery over the technological tool used (Lee, 2014). This motivation is related to the support provided by teachers in order to develop in online learners, along with mathematics teaching, the skills needed to use the selected technology (Ku et al., 2011; Nuangchalerm et al., 2011). To increase students’ motivation and evolution in a distance mathematics course, it is important to provide guidance that allows them to adapt to all technological tools used in the course (Cho & Heron, 2015). The design of support tools in online tutorials will benefit students, even in learning sequences explaining how to use technological sequences that will be employed in the mathematics course. All these aspects can be discussed during the first class session and, if need arises, continuously during other teaching sequences. The goal is to reduce students’ emotional frustrations by enabling them to focus on the mathematical learning content instead of the technological tools for distance learning (Cho & Heron, 2015).
In addition to the support related to technological tools, teachers’ availability also constitutes a major factor for mathematics distance learning (Lee, 2014; Russell et al., 2009). According to these authors, distance learning in mathematics should rely on tools and strategies that would maintain interactions between the teacher and the students on a regular basis. Lee (2014) cites, inter alia, online forums, live chats, webinars, and virtual meeting times where students ask questions to improve their understanding of the course concepts. These tools might be used to encourage communication, which is essential in affecting artifact variables for mathematics teaching-learning. In fact, the communication “in math education is critically important since it promotes students’ reasoning and proof abilities along with their collaborative skills as they share their own mathematical ideas and listen to their peers’ perspectives” (Lee, 2014, p. 126). Therefore, by creating a virtual communication community, students can share their modification, emotions, and learning strategies, and they can also regulate their learning (Cho & Heron, 2015). The teacher will have relevant elements to link distance learning to students’ needs.
The appropriation of several assessment environments, an effect of the artifact variables, would allow the teacher to interact with students, monitor their learning process, motivate them, and communicate with them as needed. Actually, “assessment in education is the process of obtaining, organizing and presenting information about what and how the student is learning. Assessment uses several techniques during the teaching-learning process, and it is especially useful when evaluating open-answer questions since they allow teachers to better understand the assimilation of the student in the subject” (Farrús & Costa-jussà, 2013, p. 240). Many assessment tools are available in learning environments and choosing one tool or another must depend on several parameters. After all, assessment tools to be used in distance learning in mathematics are determined through prior analysis of the assessment sequences and students’ anxiety levels. The analysis of assessment sequences is carried out during anticipation activities and helps to identify mathematical and technological tools needed to define how information about the quality of students’ learning process are obtained, presented, and organized. Meanwhile, analyzing students’ anxiety levels helps in choosing assessments that will lead to lower levels of anxiety (Hewson, 2012). The assessment tools selected should facilitate the use and manipulation of mathematical symbols and representations. They must allow the teacher to observe and analyze students’ reasoning. In an online learning environment, assessment tools should also enable students to self-assess at any time and to receive immediate feedback (Farrús & Costa-jussà, 2013). These tools should enable the teacher to target assessment questions that appear most difficult for the students. This will allow the teacher to personally intervene when students face difficulties, notably those observed in their assessments.
Unlike Brown et al. (1999), we observed that online assessment does not reduce the teachers’ work. The evaluation of mathematics teaching cannot be limited to the automation of assessment tasks; it goes far beyond that. As a matter of fact, summative assessment cannot be limited to multiple-choice questions; nor can formative assessment. The purpose of assessment in mathematics is to observe the development of students’ conceptual understanding. Assessment through multiple-choice questions does not allow one to observe how students build their knowledge. In distance synchronous or asynchronous learning in mathematics, assessment is a key element in observing students’ learning difficulties and misunderstandings. The assessment therefore allows the teacher’s involvement in the students’ learning process by situating the teacher on the concepts on which it will be necessary to dwell again. It is essential for preservice teachers’ initial training to be based on assessment techniques and tools that can be used to observe students’ reasoning.
In short, the nature of mathematical knowledge greatly determines the technological tools to use for distance learning. Artifact variables serve to interpret how to choose, use, evaluate, and revise technological tools for mathematics distance learning. They are focused on the use, manipulation, and presentation of mathematical symbols or figures based on the mathematical knowledge to build. These variables must be discussed during initial training as the appropriation process of knowledge about the use of technological tools for the distance learning of curricular content. These best effects are therefore related to curricular content, the development of conceptual understanding, and students’ motivation. Artifact variables are thus greatly influenced by arrangement variables.
Arrangement variables of the anticipation genesis for distance learning is a scenario system of didactic exploitation that is operationalized through the following: (a) the analysis of students’ possible errors and their didactic or epistemological origin; (b) the adaptation of curricular content; (c) the way concepts are explained (the meaning given to concepts or to their formulas, different representations of concepts); (d) the interpretation of concepts; (e) the problems related to providing context; (f) the way tasks, definitions, and characteristics are presented; (g) the way teaching is introduced; and (h) the organization of the education period (Nongni, 2020). These eight characteristics of arrangement variables influence the technological tools to use for asynchronous or synchronous mathematics teaching. During anticipation activities for distance learning of a mathematical concept, teachers must first define the orientations of the concepts to teach based on each of the eight operationalization characteristics of arrangement variables. It is following the analysis of the eight characteristics based on the concept to teach that the teacher will identify technological tools that will better link to the teaching needs of the concept concerned. This phase of linking technological tools depending on the concept to be remotely taught helps in observing that anticipation activities of distance learning in mathematics require extra work that is not needed in face-to-face teaching. Thus, the initial training of mathematics preservice teachers might account for this extra work. In fact, linking student needs for knowledge construction with technological tools to be used in distance learning will encourage the emergence of the teacher’s stance among preservice teachers, mainly by situating teaching-learning problems from a more constructive perspective of mathematical knowledge.
The selection of task types is a component of arrangement variables to consider when teaching mathematics remotely. In effect, routine problems and problems centred on calculation procedures seem to disengage students during a remote mathematics course, particularly in a synchronous mode (Francis & Jacobsen, 2013). Thus, in anticipatory activities for teaching mathematics in a synchronous mode, the above-mentioned tasks must occupy little space. They might be used for students’ homework. Activities selected during teaching anticipations could enhance the development of students’ conceptual understanding. For instance, a multifaceted presentation of mathematical concepts, discovery-centred tasks, tasks focused on collaborative problem-solving, and active learning-oriented tasks would promote a more engaged mathematical space (Francis & Jacobsen, 2013).
Moreover, motivation and self-efficacy greatly influence student engagement (Cho & Heron, 2016). To promote student engagement, it appears necessary to identify the tasks that interest students. Adapting tasks according to the students’ interests is an effect of the arrangement variables. In fact, taking into account students’ interests during anticipation activities enhances the choice of the learning context. However, mathematics teacher training, in relation to the context, remains a major challenge (Balhan et al., 2019; Ben-Zvi & Makar, 2016; Djeumeni, 2015; Proulx & Bednarz, 2010). For example, research conducted with 12 Cameroonian preservice teachers reveals that preservice teachers’ problems with tasks that might interest students are focused on their experiences as a former student, their personal experiences, and their beliefs (Nongni, 2020). This seems to keep preservice teachers away from the teacher’s stance, where surveys of students are encouraged to determine their interests. The teacher’s stance also enhances the environmental context of technological tools so that preservice teachers continuously adapt to individual differences between students. It equally takes into account interdisciplinary challenges that interest students. Note also that difficulties faced by preservice teachers in regard to students’ interests are equally influenced by their teaching difficulties (Nongni, 2020). This result enriches that of Queiroz et al. (2017), who conducted interviews with preservice teachers regarding their knowledge of, background in, and experience with statistics. They then observed the predominance of their previous and personal experiences on their point of views about contexts and tasks. We can therefore confirm the hypothesis left open by Queiroz et al. (2017): that former students’ experiences and trainees’ personal experiences would have implications in their anticipation activities when planning teaching. In the context of distance learning, challenges related to recognizing tasks that lead to student engagement become more important in influencing the different arrangement variables. Initial training could prepare preservice teachers to efficiently work on student engagement. It should allow preservice teachers to move from their conception of contextualization that remains focused on the stance of former students to a conception of contextualization oriented towards the stance of the teacher. Preservice teachers must in fact be flexible to understand their students’ contextual needs in order to anticipate solutions that could be useful for students’ learning (Chinnappan, 2006).
Arrangement variables in mathematics distance learning help the preservice teachers and the teachers to observe deeply how technological resources can influence teaching a mathematical concept. Consequently, the selection of technological tools for distance teaching and learning and of the components of artifact variables can influence the implementation of arrangement variables. The technological tools employed have an impact on the components of arrangement variables such as the recognition of tasks that interest students, the multifaceted presentation of concepts, the anticipation of tasks facilitating the introduction of the teaching, the anticipation of definitions, and data interpretation (Nongni, 2020). Furthermore, arrangement variables can also influence and initiate the use of didactic variables, variability, and dispersed data, all of which are related to the nature of the data. In fact, Nongni (2020) has observed in 12 Cameroonian preservice teachers who plan to teach statistics that their anticipated tasks highlight changes of modality values to enable studying these concepts from several angles. These tasks are characterized by, inter alia, discrete and continuous data, problem situations of addition and multiplication of modalities by the same number, and situations of using data from the students' social reality. This is how arrangement variables implementing concepts from various angles lead to the use of variables related to the nature of the data.
Variables related to the nature of the data of the anticipation genesis for distance learning concern data used to enhance students’ conceptual understanding. They are operationalized in anticipation activities through the following: (a) the use of didactic variables; (b) the use of real-life data; (c) the collection of data by students; (d) the gathering of the data; (e) the use of various data (dispersed, undispersed, continuous, discrete, etc.); and (f) variability of the data (Nongni, 2020). Employing these variables encourages the implementation of arrangement variables that serve to anticipate tasks, by presenting the concepts to be taught in several facets (Nongni, 2020). During anticipation activities of mathematics distance learning, the valorization of the variables’ components linked to the nature of the data assist in orientating planning towards students’ knowledge construction. They will thus allow students to adapt and regulate their knowledge. In the context of distance learning, however, manipulating variables related to the nature of the data is not obvious. Indeed, it seems more difficult for the teacher to observe in a real way how students perform the learning tasks. Therefore, the data to be used should be diverse and clearly identified in the tasks. Furthermore, continuous and frequent formative assessments constitute a key element to regulate students’ knowledge based on variables related to the data’s nature.
We have analyzed how mathematics teachers’ initial training could prepare them to anticipate the challenges if distance learning. In this vein, the anticipation genesis of planning mathematics distance learning has been defined (see Figure 1).
Figure 1
Schematic Representation of the Anticipation Genesis in the Planning of Teaching

This approach, called anticipatory genesis, extends the documentary genesis of Gueudet and Trouche (2008). It is also part of the documentational approach to didactics perspective (Drijvers et al., 2019) and the design linking the stances that teachers can adopt with learning materials (Leroyer, 2018a, 2018b), in particular, at the level of initial training for mathematics distance learning. The innovation of this approach is that it makes defining how to plan the teaching of mathematical distance learning possible, in particular, by highlighting the interplay between the planning variables and the epistemological postures adopted by preservice teachers. This approach sheds light on the role of planning in mathematics distance learning, differentiating between staying in contact with mathematics remotely and mathematics distance learning. It is easy to stay in contact with mathematics remotely. Besides, many solutions and tools exist to give students the opportunity to stay connected to mathematics. Mathematics distance learning goes beyond contact with mathematics, it focuses on the students’ development of conceptual, cognitive, and meta-cognitive understandings. It is thanks to the conceptual analysis of the knowledge to teach, of students’ difficulties and knowledge, and of teaching-learning pedagogical resources that we can determine the technological tools to be used in distance learning. Thus, linking technological tools depending on the concept to be remotely taught helps in observing that mathematics distance learning requires an extra work that is not needed in face-to-face teaching. So, to better prepare primary or secondary preservice teachers to teach mathematics remotely, initial training should enable them to move towards the teacher’s stance by enhancing students’ understanding and interpretation.
It seems necessary to multiply, during the preservice training programs, the moments of discussion on the different knowledge feeding the practices of mathematics distance learning. Indeed, given that preservice teachers show resistance to less familiar practices (Clift & Brady, 2005), it is interesting to develop courses that are fully and essentially grounded in mathematics distance learning and that allow for in-depth exploration of mathematical concepts: this is the new challenge of preservice training programs. These courses should focus on didactic knowledge regarding the teaching of mathematical concepts at a distance. They will therefore complement educational technology courses and courses focused on planning that currently exist in preservice training programs and are very general in nature. Indeed, since the emergence of the teacher’s stance among preservice teachers is reciprocally influenced by the components of artifact variables, arrangement variables, and variables related to the nature of the data, it seems important to study how to teach each mathematical concept at a distance. This does not mean putting face-to-face courses online but rather highlighting the development of conceptual understanding during distance learning. Although this research is limited to the analysis of several scientific studies, the underlying theoretical framework allows us to conclude that teaching each mathematical concept should be rethought and questioned in the context of distance learning.
To specifically support the theoretical framework developed in this article, it is essential for future research to collect and analyze data on the distance learning of each mathematics concept. This will allow us to see how the variables discussed are specifically presented and how they could be enhanced in order for each concept to be taught.
Adler, J. (2010). La conceptualisation des ressources. Apports pour la formation des professeurs de mathématiques [Conceptualizing resources. Contributions to the training of mathematics teachers]. In G. Gueudet & L. Trouche (Eds.), Ressources vives. Le travail documentaire des professeurs en mathématiques (pp. 23-37). Presses Universitaires de Rennes et INRP.
Balhan, K., Gerard, I., Ngan, G. N., & Schneider, M. (2019). Une dimension particulière de la réflexivité: “les mathématiques comme problème professionnel” à la base d’un dispositif de formation initiale en didactique des mathématiques [A particular dimension of reflexivity: "mathematics as a professional problem" at the basis of an initial training program in mathematics education]. Canadian Journal of Science, Mathematics and Technology Education, 19(2), 1-13. https://doi.org/10.1007/s42330-018-0035-y
Ben-Zvi, D., & Makar, K. (2016). International perspectives on the teaching and learning of statistics. In D. Ben-Zvi & K. Makar (Eds.), The teaching and learning of statistics (pp. 1-10). Springer.
Bergeron, L. (2016). La planification de l’enseignement et la gestion pédagogique de la diversité des besoins des élèves en classe ordinaire: une recherche collaborative au primaire [Teaching planning and pedagogical management of students' diverse needs in the regular classroom: collaborative research in the elementary school]. Thèse de doctorat. Université du Québec à Trois-Rivières. http://depot-e.uqtr.ca/id/eprint/8015/
Brousseau, G. (1998). Théorie des situations didactiques [The theory of didactical situations]. La pensée sauvage.
Brown, S., Race, R., & Bull, J. (1999). Computer-assisted assessment in higher education. Koganm.
Cabon, P., Delgoulet, C., & Valot, C. (2014). Quelques approches du processus d’anticipation en ergonomie: de l’individu à l’organisation [Some approaches to the anticipation process in ergonomics: from the individual to the organization]. In E. Siéroff, E. Drozda-Senkowska, A. M. Ergis, & S. Moutier (Eds.), Psychologie de l’anticipation (pp. 37-55). Armand Colin.
Chinnappan, M. (2006). Using the productive pedagogies framework to build a community of learners online in mathematics education. Distance Education, 27(3), 355-369. https://doi.org/10.1080/01587910600940430
Cho, M. H., & Heron, M. L. (2015). Self-regulated learning: The role of motivation, emotion, and use of learning strategies in students’ learning experiences in a self-paced online mathematics course. Distance Education, 36(1), 80-99. https://doi.org/10.1080/01587919.2015.1019963
Clerc, A., & Martin, D. (2011). L’étude collective d’une leçon, une démarche de formation pour développer et évaluer la construction des compétences professionnelles des futurs enseignants [The collective study of a lesson, a training approach to develop and evaluate the construction of professional skills of preservice teachers]. Revue internationale de pédagogie de l’enseignement supérieur, 27(2), 2-13. https://doi.org/10.4000/ripes.514
Clift, R., & Brady, P. (2005). Research on methods courses and field experiences. In M. Cochran-Smtih & K. Zeichner (Eds.), Studying teacher education: The report of the AERA panel on research and teacher education (pp. 309-424). American Educational Research Association.
Cohan, A., & Honigsfeld, A. (2006). Incorporating “lesson study” in teacher preparation. The Educational Forum, 71(1), 81-82. https://doi.org/10.1080/00131720608984570
CSE: Conseil supérieur de l’éducation. (2020). Éduquer au numérique: Rapport sur l’état et les besoins de l’éducation 2018-2020 [Educating digitally: a report on the state and needs of education 2018-2020]. Québec, Le Conseil. https://www.cse.gouv.qc.ca/publications/eduquer-au-numerique-50-0534/#:~:text=Dans%20son%20rapport%20sur%20l,pour%20le%20syst%C3%A8me%20d’%C3%A9ducation
DeBlois, L. (2012). De l’ancien élève à l’enseignant. Quel parecours [From former student to teacher. What a path]. In J. Proulx, C. Corriveau, & H. Squalli (Eds.), Formation mathématique pour l’enseignement des mathématiques (pp. 313-320). Presses de l’Université du Québec.
DeBlois, L., & Squalli, H. (2002). Implication de l’analyse de productions d’élèves dans la formation des maitres du primaire [Implication of the analysis of students' productions in the training of primary school teachers]. Educational Studies in Mathematics, 50(2), 212-237. https://www.jstor.org/stable/3483299?seq=1
Diallo, P. (2005). Savoir-enseigner et approche constructiviste des apprentissages en formation initiale des maîtres: Les paramètres du développement professionnel dans les productions étudiantes des futurs enseignants Franco-Ontariens [Knowing how to teach and the constructivist approach to learning in initial teacher training: The parameters of professional development in the productions of preservice Franco-Ontarian teachers]. Canadian Journal of Educational Administration and Policy, 39, 1-15. https://cdm.ucalgary.ca/index.php/cjeap/article/view/42719
Djeumeni, M. (2015). La formation pratique des enseignants au Cameroun [Practical teacher training in Cameroon]. Formation et profession, 23(3), 169-180. https://doi.org/10.18162/fp.2015.a77
Drijvers, P., ... Nongni, G., ... et Rodrigues, A. (2019). Transitions Toward Digital Resources: Change, Invariance, and Orchestration. In: Trouche L., Gueudet G., Pepin B. (Eds.), The 'Resource' Approach to Mathematics Education. Advances in Mathematics Education. Springer, Cham. https://doi.org/10.1007/978-3-030-20393-1_12
Dumouchel, G., & Karsenti, T. (2013). Les compétences informationnelles relatives au Web des futurs enseignants québécois et leur préparation à les enseigner: résultats d’une enquête [Computer/Internet skills of preservice teachers in Québec and their readiness to teach them: survey results]. Éducation et Francophonie, 41(1), 7-29. https://doi.org/10.7202/1015057ar
Farrús, M., & Costa-jussà, M. R. (2013). Automatic evaluation for e-learning using latent semantic analysis: A use case. International Review of Research in Open and Distributed Learning, 14(1), 239-254. https://doi.org/10.19173/irrodl.v14i1.1389
Francis, K., & Jacobsen, M. (2013). Synchronous online collaborative professional development for elementary mathematics teachers. The International Review of Research in Open and Distributed Learning, 14(3), 319-343. https://doi.org/10.19173/irrodl.v14i3.1460
Gattuso, L. (1993). Les conceptions personnelles au sujet de l’enseignement des mathématiques et leur reflet dans la pratique: Un essai d’autoanalyse [Personal conceptions about mathematics education and their reflection in practice: An attempt at self-analysis]. [Doctoral dissertation, Université de Montréal]. https://www.elibrary.ru/item.asp?id=5685147
Gueudet, G., & Trouche, L. (2008). Du travail documentaire des enseignants: Genèses, collectifs, communautés. Le cas des mathématiques [On teachers' documentary work: Geneses, collectives, communities. The case of mathematics]. Éducation et Didactique, 2(3), 7-33. https://doi.org/10.4000/educationdidactique.342
Gueudet, G., & Trouche, L. (2010). Des ressources aux documents, travail du professeur et genèses documentaires [From resources to documents, teacher's work and documentary genesis]. In G. Gueudet & L. Trouche (Eds.), Ressources vives. Le travail documentaire des professeurs en mathématiques (pp. 57-74). Presses Universitaires de Rennes et INRP.
Hewson, C. (2012). Can online course-based assessment methods be fair and equitable? Relationships between students’ preferences and performance within online and offline assessments. Journal of Computer Assisted Learning, 28, 288-298. https://doi.org/10.1111/j.1365-2729.2011.00473.x
Hodges, C., Moore, S., Lockee, B., Trust, T., & Bond, A. (2020, March 27). The difference between emergency remote teaching and online learning. EDUCAUSE Review. https://er.educause.edu/articles/2020/3/the-difference-between-emergency-remote-teaching-and-online-learning
Ku, H., Akarasriworn, C., Glassmeyer, D. M., Mendoza, B., & Rice, L. A. (2011). Teaching an online graduate mathematics education course for in-service mathematics teachers. Quarterly Review of Distance Education, 12(2), 135-147. https://go.gale.com/ps/anonymous?id=GALE%7CA284222195&sid=googleScholar&v=2.1&it=r&linkaccess=abs&issn=15283518&p=AONE&sw=w
Lee, J. (2014). An exploratory study of effective online learning: Assessing satisfaction levels of graduate students of mathematics education associated with human and design factors of an online course. International Review of Research in Open and Distributed Learning, 15(1), 111-132. https://doi.org/10.19173/irrodl.v15i1.1638
Legendre, R. (2005). Dictionnaire actuel de l’éducation [Current Dictionary of Education] (3rd ed.). Guérin.
Leroyer, L. (2018a). The capacity to think of transmission of knowledge from learning supports: A proposition of a conceptual model. In V. Gitirana, T. Miyakawa, M. Rafalska, S. Soury-Lavergne, & L. Trouche (Eds.), Proceedings of the re(s)sources 2018 international conference (pp. 203-206). ENS de Lyon.
Leroyer, L. (2018b, October 22-26). La notion de support, au centre d’un modèle des situations d’enseignement/apprentissage, ressource pour comprendre et pour faire [The notion of support, at the center of a model of teaching/learning situations, a resource for understanding and doing]. In Espace mathématique francophone 2018 (EMF). GT6: Conception, diffusion et usages des ressources (pp. 98-105). Gennevilliers, France.
Malo, A. (2000). Savoirs de formation et savoirs d’expérience: un processus de transformation [Training knowledge and experience knowledge: a process of transformation]. Éducation et Francophonie, 28(2), 216-235. http://collections.banq.qc.ca/ark:/52327/bs61547
Morin, M. P. (2008). Les connaissances mathématiques et didactiques chez les futurs maîtres du primaire: Quatre cas à l’étude [The mathematical and didactic knowledge of primary preservice teachers: Four case studies]. Canadian Journal of Education/Revue Canadienne de l’Éducation, 31(3), 537-566. https://journals.sfu.ca/cje/index.php/cje-rce/article/view/3012
Ndolly, G. (2012). L’apprentissage à l’enseignement de la géométrie: analyse des pratiques de futurs enseignants en stage à l’école primaire au Gabon [Learning to teach geometry: analysis of the practices of primary pre-service teachers in Gabon]. [Doctoral dissertation, Université Laval Bibliothèque]. https://corpus.ulaval.ca/jspui/handle/20.500.11794/23261
Nongni, G. (2020). Intégration des ressources documentaires numériques dans la planification de l’enseignement de la statistique par des futurs enseignants au secondaire [Integration of digital documentary resources in the planning of statistics education by secondary preservice teachers]. [Doctoral dissertation, Université Laval]. https://corpus.ulaval.ca/jspui/handle/20.500.11794/38214
Nuangchalerm, P., Prachagool, V., & Sriputta, P. (2011). Online professional experiences in teacher preparation program: A preservice teacher study. Canadian Social Science, 7(5), 116-120. https://doi.org/10.3968/J.css.1923669720110705.298
Proulx, J., & Bednarz, N. (2010). Formation mathématique des enseignants du secondaire. Partie 1: Réflexions fondées sur une analyse des recherches [Mathematics Education for Secondary School Teachers. Part 1: Reflections based on a review of research]. Revista de Educação Matemática eTecnologica Ibero-americana, 1(1), 1-23. https://periodicos.ufpe.br/revistas/index.php/emteia/article/viewFile/2271/1833
Queiroz, T., Monteiro, C., Carvalho, L., & François, K. (2017). Interpretation of statistical data: The importance of affective expressions. Statistics Education Research Journal, 16(1), 163-180. https://iase-web.org/documents/SERJ/SERJ16(1)_Queiroz.pdf
Rabardel, P. (1995). Les hommes et les technologies: Approche cognitive des instruments contemporains [People and technology: A cognitive approach to contemporary instruments]. Armand Colin.
Rabardel, P. (1999). Éléments pour une approche instrumentale en didactique des mathématiques [Elements for an instrumental approach in mathematics education]. Actes de L’école D’été de Didactique des Mathématiques, 2, 203-213. https://www.rabardel.fr/app/download/14429086135/1999-Rabardel-ARDM.pdf?t=1589991217
Rogers, P. L. (2009). Encyclopedia of distance learning (2nd ed.). Idea Group Inc (IGI).
Russell, M., Kleiman, G., Carey, R., & Douglas, J. (2009). Comparing self-paced and cohort-based online courses for teachers. Journal of Research on Technology in Education, 41(4), 443-466. https://doi.org/10.1080/15391523.2009.10782538
Savard, A. (2014). Enseigner à enseigner: regards croisés sur l’épistémologie et le rapport au savoir d’une professeure [Teaching to teach: crossed views on epistemology and a teacher's relationship to knowledge]. In M.-C. Bernard, A. Savard, & C. Beaucher (Eds.), Le rapport aux savoirs: une clé pour analyser les épistémologies enseignantes et les pratiques de classe. Québec: Livres en ligne du CRIRES (pp. 77-91). https://lel.crires.ulaval.ca/oeuvre/une-cle-pour-analyser-les-epistemologies-enseignantes-et-les-pratiques-de-classe
Tochon, F. (2013). Planification ouverte de l’enseignement dans une approche profonde de l’apprentissage. Le défi que les réformes en cours posent aux enseignants et aux administrations [Open planning of teaching in a deep approach to learning. The challenge that the current reforms pose to teachers and administrations]. In M. De Kesel, M. Bouhon, J.-L. Dufays, & J. Plumat (Eds.), La planification des apprentissages. Comment les enseignants des différentes disciplines programment-ils et préparent-ils leurs cours? Cadrage de la problématique (pp. 31-62). Presses universitaires de Louvain.
Trouche, L. (2007). Chapitre 1. Environnements informatisés d’apprentissage: quelle assistance didactique pour la construction des instruments mathématiques? [Chapter 1: Computerized learning environments: what didactic assistance for the construction of mathematical instruments]. In R. Floris (Ed.), Environnements informatiques, enjeux pour l’enseignement des mathématiques: Intégrer des artefacts complexes, en faire des instruments au service de l’enseignement et de l’apprentissage (pp. 19-38). De Boeck Supérieur.
UNESCO. (2020a, March 21). COVID-19: L’UNESCO organise un webinaire sur l’éducation consacré à l’équité dans la scolarité [UNESCO organizes webinar on equity education and schooling]. https://fr.unesco.org/news/covid-19-lunesco-organise-webinaire-leducation-consacre-lequite-scolarite
UNESCO. (2020b, March 30). Webinaire sur le COVID-19: Un monde nouveau s’ouvre aux enseignants, en première ligne de l’éducation [A new world for teachers, education’s frontline workers - COVID-19 education webinar]. https://fr.unesco.org/news/webinaire-covid-19-monde-nouveau-souvre-aux-enseignants-premiere-ligne-leducation
Vergnaud, G. (1990). La théorie des champs conceptuels [The Conceptual Fields' Theory]. Recherches en Didactique des Mathématiques, 10(2-3), 133-170. https://revue-rdm.com/2005/la-theorie-des-champs-conceptuels/
Vergnaud, G. (1994). Le rôle de l’enseignant à la lumière des concepts de schème et de champ conceptuel [The role of the teacher in light of the concepts of pattern and conceptual field]. Vingt ans de didactique des mathématiques en France, Grenoble, La Pensée Sauvage (pp. 177-191). La Pensée Sauvage Éditions Grenoble.

New Challenge for Initial Training of Mathematics Teachers: The Planning Phase of Mathematics Distance Learning by Gaël Nongni is licensed under a Creative Commons Attribution 4.0 International License.